Angle Bisector Perpendicular Bisector Median Altitude
Kalali
Mar 31, 2025 · 6 min read
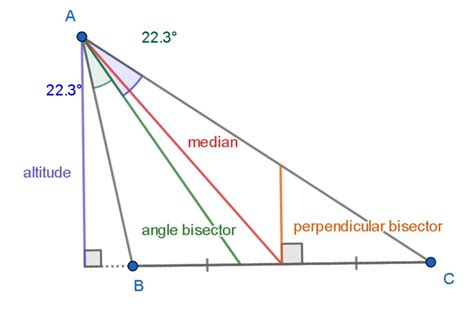
Table of Contents
Angle Bisector, Perpendicular Bisector, Median, and Altitude in Geometry
Understanding the fundamental concepts of angle bisectors, perpendicular bisectors, medians, and altitudes is crucial for mastering geometry. These lines hold unique properties and play significant roles in various geometric proofs and constructions. This comprehensive guide will delve into each concept, exploring their definitions, properties, and applications, with a special focus on their relationships within triangles.
Angle Bisector
An angle bisector is a line segment that divides an angle into two congruent angles. It originates from the vertex of the angle and extends to intersect the opposite side. In a triangle, each angle has an angle bisector.
Properties of Angle Bisectors
-
Equidistant from Sides: A point on the angle bisector is equidistant from the two sides of the angle. This is a key property often used in geometric proofs. Consider a point P on the angle bisector of ∠A. The perpendicular distances from P to the sides of ∠A are equal.
-
Intersection Point: The angle bisectors of a triangle are concurrent (they intersect at a single point). This point of intersection is called the incenter.
-
Incenter and Incircle: The incenter is the center of the incircle, which is the circle inscribed within the triangle and tangent to all three sides. The radius of the incircle is the distance from the incenter to each side of the triangle.
-
Applications: Angle bisectors are used in numerous applications, including finding the center of a circle inscribed in a triangle, dividing angles into equal parts, and solving various geometric problems.
Perpendicular Bisector
A perpendicular bisector is a line that intersects a line segment at its midpoint and forms a right angle (90 degrees) with it. It divides the line segment into two equal parts.
Properties of Perpendicular Bisectors
-
Equidistant from Endpoints: Any point on the perpendicular bisector of a line segment is equidistant from the endpoints of that segment. This property is fundamental to many geometric constructions and proofs.
-
Intersection Point: In a triangle, the perpendicular bisectors of the sides are concurrent. Their point of intersection is called the circumcenter.
-
Circumcenter and Circumcircle: The circumcenter is the center of the circumcircle, which is the circle that passes through all three vertices of the triangle. The radius of the circumcircle is the distance from the circumcenter to each vertex.
-
Right Triangles: The perpendicular bisector of the hypotenuse of a right-angled triangle is equidistant from all three vertices, and its length is half the length of the hypotenuse.
-
Applications: Perpendicular bisectors are widely used in constructing geometric shapes, finding the center of a circle that circumscribes a triangle, and solving problems related to distance and symmetry.
Median
A median of a triangle is a line segment joining a vertex to the midpoint of the opposite side. Each vertex has a corresponding median.
Properties of Medians
-
Centroid: The medians of a triangle are concurrent. Their point of intersection is called the centroid. The centroid divides each median into a ratio of 2:1, with the longer segment being closer to the vertex.
-
Center of Mass: The centroid is the center of mass of the triangle. If the triangle were a flat, uniform lamina, the centroid would be the point where it would balance perfectly.
-
Applications: Medians are used to find the centroid, which has applications in physics (center of gravity), engineering (structural design), and computer graphics (geometric modeling).
Altitude
An altitude of a triangle is a line segment from a vertex that is perpendicular to the opposite side (or its extension). Each vertex has a corresponding altitude. The opposite side is called the base, and the altitude represents the perpendicular height of the triangle.
Properties of Altitudes
-
Orthocenter: The altitudes of a triangle are concurrent, meaning they intersect at a single point. This point of intersection is called the orthocenter.
-
Acute, Obtuse, and Right Triangles: The location of the orthocenter varies depending on the type of triangle:
- Acute Triangle: The orthocenter lies inside the triangle.
- Right Triangle: The orthocenter coincides with the vertex of the right angle.
- Obtuse Triangle: The orthocenter lies outside the triangle.
-
Applications: Altitudes are crucial for calculating the area of a triangle (Area = 1/2 * base * height), and are fundamental in various geometric proofs and constructions. They are also important in trigonometry and coordinate geometry.
Interrelationships and Applications
While each of these lines – angle bisector, perpendicular bisector, median, and altitude – has unique properties, they often interact in interesting ways, particularly within the context of specific types of triangles (e.g., equilateral, isosceles, right-angled triangles).
For instance, in an isosceles triangle, the altitude from the vertex angle is also the angle bisector and the median to the base. In an equilateral triangle, all three angle bisectors, perpendicular bisectors, medians, and altitudes coincide. This is because of the inherent symmetry within these triangles.
The relationships between these lines provide powerful tools for solving geometric problems. Understanding these relationships allows us to deduce properties of a triangle given information about one or more of these lines. For example, knowing the location of the orthocenter can help determine the type of triangle. Knowing the lengths of the medians can help determine the area of the triangle.
Beyond their use in solving geometric problems, these concepts have far-reaching applications in various fields. They are fundamental to surveying, architecture, engineering, and computer graphics. In computer graphics, for instance, algorithms use these geometric principles for modeling, rendering, and manipulating three-dimensional objects.
Furthermore, understanding these concepts lays a strong foundation for advanced geometric topics like projective geometry and non-Euclidean geometry.
Advanced Concepts and Further Exploration
This exploration provides a solid foundation in the basic properties of angle bisectors, perpendicular bisectors, medians, and altitudes. Further investigation might include:
-
Exploring the properties of these lines in specific types of quadrilaterals. How do these lines behave in squares, rectangles, rhombuses, and other quadrilaterals?
-
Investigating the use of these lines in coordinate geometry. How can we use coordinates to represent and analyze these lines? How can we find the equations of these lines?
-
Examining the applications of these lines in three-dimensional geometry. How do these concepts extend to tetrahedra and other three-dimensional shapes?
-
Delving into the use of these concepts in advanced geometric proofs and theorems. How can these lines be used to solve complex geometric problems and prove important theorems?
By delving deeper into these areas, you can significantly expand your understanding of geometric principles and their applications across a wide range of disciplines. The mastery of these fundamental concepts provides a solid base for tackling more advanced geometric challenges and unlocking a deeper appreciation of the elegance and power of geometry.
Latest Posts
Latest Posts
-
Does A Stretched Bow And Arrow Have Energy
Apr 02, 2025
-
How Many Cups Is 33 Oz
Apr 02, 2025
-
Cuanto Es 10 Millas En Kilometros
Apr 02, 2025
-
How Many Cm Is 71 Inches
Apr 02, 2025
-
How Tall Is 65inches In Feet
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Angle Bisector Perpendicular Bisector Median Altitude . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
