Angles Formed By Chords Secants And Tangents
Kalali
Mar 30, 2025 · 6 min read
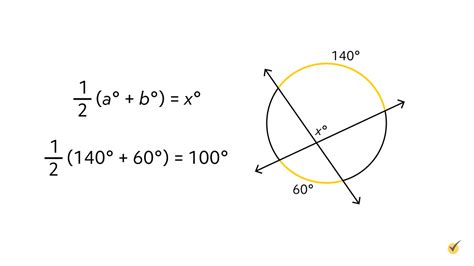
Table of Contents
Angles Formed by Chords, Secants, and Tangents: A Comprehensive Guide
Geometry, a cornerstone of mathematics, unveils fascinating relationships within shapes and figures. Among the most intriguing aspects are the angles formed by the intersection of chords, secants, and tangents within a circle. Understanding these relationships is crucial for solving various geometric problems and deepening your understanding of circular geometry. This comprehensive guide delves into the theorems and formulas governing these angles, providing clear explanations and illustrative examples.
Understanding the Basics: Chords, Secants, and Tangents
Before diving into the angle relationships, let's clarify the definitions of the key components:
-
Chord: A straight line segment whose endpoints both lie on the circle's circumference. A diameter is a special chord that passes through the center of the circle.
-
Secant: A straight line that intersects the circle at two distinct points. A secant extends beyond the circle's circumference, unlike a chord which is entirely contained within the circle.
-
Tangent: A straight line that touches the circle at exactly one point, called the point of tangency. The tangent line is perpendicular to the radius drawn to the point of tangency.
Angles Formed by Intersecting Chords
When two chords intersect inside a circle, they form four angles. The measure of each angle formed is half the sum of the measures of the intercepted arcs.
Theorem: The measure of an angle formed by two intersecting chords inside a circle is half the sum of the measures of the intercepted arcs.
Formula: Let the angle be denoted as θ, and the intercepted arcs as arc A and arc B. Then:
θ = (1/2) * (arc A + arc B)
Example: If two chords intersect inside a circle, forming an angle of 50°, and one intercepted arc measures 60°, what is the measure of the other intercepted arc?
Using the formula: 50° = (1/2) * (60° + arc B) => 100° = 60° + arc B => arc B = 40°
Angles Formed by a Tangent and a Chord
A tangent intersecting a chord at the point of tangency forms an interesting relationship with the intercepted arc.
Theorem: The measure of an angle formed by a tangent and a chord at the point of tangency is half the measure of the intercepted arc.
Formula: Let the angle be denoted as θ, and the intercepted arc as arc A. Then:
θ = (1/2) * arc A
Example: If a tangent and a chord intersect at a point on the circle, forming an angle of 35°, what is the measure of the intercepted arc?
Using the formula: 35° = (1/2) * arc A => arc A = 70°
Angles Formed by Two Secants
When two secants intersect outside a circle, they form four angles. The measure of the angle formed outside the circle is half the difference of the measures of the intercepted arcs.
Theorem: The measure of an angle formed by two secants intersecting outside a circle is half the difference of the measures of the intercepted arcs.
Formula: Let the angle formed outside the circle be θ, the larger intercepted arc be arc A, and the smaller intercepted arc be arc B. Then:
θ = (1/2) * (arc A - arc B)
Example: Two secants intersect outside a circle, forming an angle of 25°. If the larger intercepted arc measures 110°, what is the measure of the smaller intercepted arc?
Using the formula: 25° = (1/2) * (110° - arc B) => 50° = 110° - arc B => arc B = 60°
Angles Formed by a Secant and a Tangent
When a secant and a tangent intersect outside a circle, they also form an angle related to the intercepted arcs. The formula is similar to that of two intersecting secants.
Theorem: The measure of an angle formed by a secant and a tangent intersecting outside a circle is half the difference of the measures of the intercepted arcs.
Formula: Let the angle formed outside the circle be θ, the larger intercepted arc be arc A (on the secant), and the smaller intercepted arc be arc B (between the point of tangency and the intersection of the secant and tangent). Then:
θ = (1/2) * (arc A - arc B)
Example: A secant and a tangent intersect outside a circle, forming an angle of 40°. If the intercepted arc on the secant measures 130°, what is the measure of the intercepted arc between the point of tangency and the intersection point?
Using the formula: 40° = (1/2) * (130° - arc B) => 80° = 130° - arc B => arc B = 50°
Angles Formed by Two Tangents
Two tangents drawn from the same external point to a circle form an angle whose measure is related to the intercepted arcs.
Theorem: The measure of an angle formed by two tangents drawn from an external point to a circle is half the difference of the measures of the major and minor intercepted arcs. Alternatively, it is also the supplement of the central angle subtended by the intercepted arcs.
Formula: Let the angle formed by the tangents be θ, the major intercepted arc be arc A, and the minor intercepted arc be arc B. Then:
θ = (1/2) * (arc A - arc B) or θ = 180° - (central angle)
Example: Two tangents intersect outside a circle, forming an angle of 70°. What is the measure of the major intercepted arc if the minor intercepted arc is 50°?
Using the formula: 70° = (1/2) * (arc A - 50°) => 140° = arc A - 50° => arc A = 190°
Solving Complex Geometric Problems
These theorems provide powerful tools for solving complex geometric problems involving circles. Many problems involve combining these theorems and using other geometric principles to find unknown angles, arc measures, or segment lengths. Practice is key to mastering the application of these concepts.
Advanced Applications and Extensions
The concepts discussed extend beyond basic geometric problem-solving. They have applications in:
-
Calculus: Understanding angles formed by tangents and secants is crucial in calculating derivatives related to curves and circles.
-
Computer Graphics: These theorems are fundamental in algorithms for rendering and manipulating circular shapes in computer graphics applications.
-
Engineering and Architecture: Designing circular structures and calculating angles in various applications necessitates a strong understanding of these principles.
-
Physics: Calculating angles of trajectories and determining distances related to circular motion often involves application of these geometric concepts.
Practice Problems
To solidify your understanding, try solving these problems:
-
Two chords intersect inside a circle, forming angles of 40° and 140°. Find the measures of the intercepted arcs.
-
A tangent and a chord intersect at a point on a circle, forming an angle of 65°. Find the measure of the intercepted arc.
-
Two secants intersect outside a circle, forming an angle of 30°. The larger intercepted arc measures 120°. Find the measure of the smaller intercepted arc.
-
A secant and a tangent intersect outside a circle at an angle of 20°. The intercepted arc on the secant measures 100°. Find the measure of the smaller intercepted arc.
-
Two tangents intersect outside a circle, forming an angle of 80°. Find the measures of the intercepted arcs.
By understanding the relationships between angles and arcs formed by chords, secants, and tangents, you gain a deeper insight into the beauty and power of circular geometry. Mastering these concepts unlocks the ability to solve a wide array of geometric problems and expands your mathematical proficiency. Remember consistent practice is essential to building a strong foundation in geometry.
Latest Posts
Latest Posts
-
What Is The Least Common Multiple Of 5 And 12
Apr 01, 2025
-
2 5 Ounces Is How Many Ml
Apr 01, 2025
-
Why Does Passive Transport Not Require Energy
Apr 01, 2025
-
What Is 65 As A Fraction
Apr 01, 2025
-
How Many Miles Is 1600 Km
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about Angles Formed By Chords Secants And Tangents . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
