Any Set Of Ordered Pairs Is Called A
Kalali
Mar 30, 2025 · 6 min read
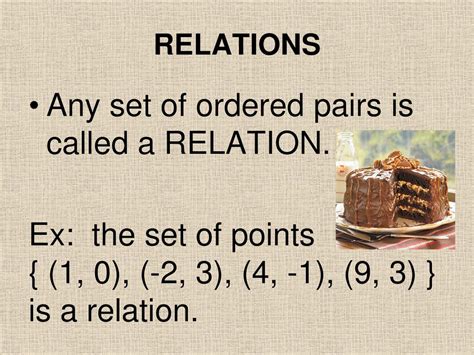
Table of Contents
Any Set of Ordered Pairs is Called a Relation
A fundamental concept in mathematics, particularly within the realms of set theory and discrete mathematics, is the notion of a relation. Understanding relations is crucial for grasping more advanced topics like functions, graphs, and databases. Simply put, any set of ordered pairs is called a relation. This seemingly simple definition unlocks a vast world of mathematical possibilities and applications. Let's delve deeper into this definition, exploring its properties, types, and significance.
Understanding Ordered Pairs
Before we dissect the definition of a relation, we need to understand the core component: the ordered pair. An ordered pair is a collection of two elements, typically denoted as (a, b), where 'a' is the first element and 'b' is the second element. The order matters; (a, b) is distinct from (b, a) unless a = b. This contrasts with sets, where {a, b} is equivalent to {b, a}.
Consider the following examples:
- (1, 2): The first element is 1, and the second element is 2.
- (apple, orange): The first element is "apple," and the second element is "orange."
- (3, 3): Both elements are 3, but the order is still significant in the context of ordered pairs.
Defining a Relation: A Set of Ordered Pairs
Now, we can formally define a relation. A relation is simply a set of ordered pairs. Each ordered pair represents a connection or relationship between the first and second elements. The elements within these pairs can belong to any set, which are often referred to as the domain and codomain (or range).
Let's illustrate with examples:
-
Example 1: A relation representing "less than" between integers:
R = {(1, 2), (1, 3), (2, 3), (-1, 0), (0, 1)}
This relation R shows instances where the first element is less than the second element. The domain is {-1, 0, 1, 2} and the codomain is {0, 1, 2, 3}.
-
Example 2: A relation representing "is a divisor of" between integers:
S = {(1, 2), (1, 3), (2, 4), (3, 6), (1, 1), (2,2), (3,3)}
Here, the relation S indicates that the first element divides the second element without leaving a remainder.
-
Example 3: A relation representing siblings:
T = {("Alice", "Bob"), ("Bob", "Alice"), ("Charlie", "David"), ("David", "Charlie")}
In this example, the relation T expresses the sibling relationship between individuals.
These examples demonstrate the versatility of relations. They can represent various types of connections – numerical comparisons, divisibility, family ties, and countless others.
Properties of Relations
Relations possess several important properties that influence their characteristics and applications:
1. Reflexivity
A relation R on a set A is reflexive if for every element a ∈ A, (a, a) ∈ R. In simpler terms, every element is related to itself.
- Example: The relation "is equal to" (=) on the set of real numbers is reflexive because every number is equal to itself.
2. Symmetry
A relation R on a set A is symmetric if for every (a, b) ∈ R, (b, a) ∈ R. If a is related to b, then b is related to a.
- Example: The relation "is equal to" (=) on the set of real numbers is symmetric. If a = b, then b = a. The relation "is a sibling of" is also symmetric (assuming we disregard the complexities of half-siblings).
3. Transitivity
A relation R on a set A is transitive if for every (a, b) ∈ R and (b, c) ∈ R, then (a, c) ∈ R. If a is related to b, and b is related to c, then a is related to c.
- Example: The relation "less than" (<) on the set of real numbers is transitive. If a < b and b < c, then a < c. The relation "is an ancestor of" is also transitive.
Combining Properties
Relations can exhibit combinations of these properties. For example, a relation that is reflexive, symmetric, and transitive is called an equivalence relation. Equivalence relations partition a set into disjoint subsets called equivalence classes. These classes are sets of elements that are all related to each other.
An example of an equivalence relation is congruence modulo n, where two integers are congruent modulo n if their difference is divisible by n.
Types of Relations
Beyond the properties mentioned above, relations are often categorized into different types based on their specific characteristics. Here are some notable examples:
- Functions: A special type of relation where each element in the domain is associated with exactly one element in the codomain. We will explore this in more detail in the following section.
- Partial Orders: Relations that are reflexive, antisymmetric (if (a, b) ∈ R and (b, a) ∈ R, then a = b), and transitive. They are used to represent orderings where not all pairs of elements are comparable.
- Total Orders (Linear Orders): A special case of partial orders where every pair of elements is comparable.
- Equivalence Relations: As mentioned earlier, these relations are reflexive, symmetric, and transitive. They partition the set into equivalence classes.
Relations and Functions: A Closer Look
Functions are a crucial subset of relations. A function is a relation where each element in the domain is associated with exactly one element in the codomain. This "one-to-one" mapping distinguishes functions from general relations.
For example, consider the relation R = {(1, 2), (2, 4), (3, 6)}. This is a function because each element in the domain {1, 2, 3} maps to exactly one element in the codomain {2, 4, 6}.
However, the relation S = {(1, 2), (1, 3), (2, 4)} is not a function because the element 1 in the domain is mapped to two elements (2 and 3) in the codomain.
Representations of Relations
Relations can be represented in several ways:
- Set Notation: The most straightforward method, as shown in the examples above.
- Matrices: A matrix can represent a relation between two finite sets. The rows and columns correspond to the elements of the sets, and an entry (i, j) is 1 if (i, j) is in the relation and 0 otherwise.
- Graphs (Directed Graphs): The elements of the sets are represented as nodes, and a directed edge from node 'a' to node 'b' indicates that (a, b) is in the relation. This visual representation is particularly helpful for understanding the structure of a relation.
- Arrow Diagrams: Similar to graphs, but often used for smaller relations to illustrate the mapping between elements.
Applications of Relations
Relations are fundamental in various areas of mathematics and computer science:
- Databases: Relational databases organize data using relations. Tables represent relations, and rows correspond to ordered pairs.
- Graph Theory: Graphs are inherently based on relations, with edges defining relationships between vertices.
- Formal Languages and Automata Theory: Relations are used to define the transitions in finite automata and other computational models.
- Order Theory: Partial orders and total orders are essential concepts in order theory, used in areas like scheduling and optimization.
- Software Engineering: Relations are implicitly used in modeling data structures and interactions in software systems.
Conclusion: The Ubiquitous Nature of Relations
The seemingly simple definition – any set of ordered pairs is called a relation – belies the profound significance of this concept. Relations provide a powerful framework for modeling relationships between elements in various contexts, from simple numerical comparisons to complex data structures in databases. Understanding the properties, types, and representations of relations is essential for mastering various mathematical and computational disciplines. Their applications are widespread, underscoring their importance as a fundamental building block in many areas of study. The versatility and power of relations make them a core concept for any serious student of mathematics or computer science. Their impact extends far beyond the theoretical, shaping the way we organize and interpret data in the modern world.
Latest Posts
Latest Posts
-
What Percentage Is 35 Out Of 50
Apr 01, 2025
-
How To Make A Velocity Vs Time Graph
Apr 01, 2025
-
Is The Atlantic Colder Than The Pacific
Apr 01, 2025
-
What Is The Warmest Part Of The Day
Apr 01, 2025
-
48 Oz Equals How Many Cups
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about Any Set Of Ordered Pairs Is Called A . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
