Area Of Non Right Angle Triangle
Kalali
Mar 28, 2025 · 5 min read
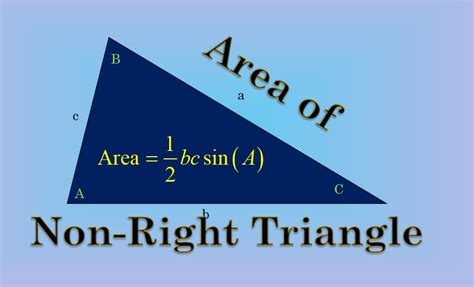
Table of Contents
Delving Deep into the Area of Non-Right Angle Triangles: A Comprehensive Guide
Determining the area of a triangle is a fundamental concept in geometry, crucial for various applications in fields ranging from surveying and architecture to computer graphics and physics. While calculating the area of a right-angled triangle is straightforward (½ * base * height), finding the area of a non-right-angled triangle requires a slightly different approach. This comprehensive guide explores the various methods available, providing clear explanations and practical examples to help you master this essential skill.
Understanding the Challenge: Why Right-Angle Formulas Fail
The simple formula (½ * base * height) works flawlessly for right-angled triangles because the base and height are perpendicular. However, in non-right-angled triangles, there's no readily apparent perpendicular height. We need alternative methods that utilize other known triangle properties. This is where several powerful formulas come into play.
Method 1: Using the Sine Rule and Heron's Formula – A Versatile Approach
This method offers a flexible solution for finding the area of any triangle, irrespective of its angles. It combines the power of the Sine Rule and Heron's Formula.
1.1. The Sine Rule:
The Sine Rule establishes a relationship between the sides and angles of a triangle:
a / sin A = b / sin B = c / sin C
where:
- a, b, c are the lengths of the sides opposite angles A, B, C respectively.
This rule is instrumental in finding the area because it allows us to determine the height of the triangle even if it isn't directly provided.
1.2. Finding the Height (h):
Let's say we want to find the height (h) from side 'a' to the opposite vertex. Using the Sine Rule, we can derive the height:
h = b * sin C (or h = c * sin B)
This formula elegantly connects the height, one side, and the opposite angle. Understanding this derivation is crucial for applying the sine rule effectively.
1.3. Heron's Formula:
Heron's Formula provides a direct route to calculating the area given only the lengths of the three sides. It avoids the need for explicitly calculating the height.
First, calculate the semi-perimeter (s):
s = (a + b + c) / 2
Then, apply Heron's Formula to calculate the area (A):
A = √[s(s-a)(s-b)(s-c)]
This formula is remarkably efficient and is often preferred when the side lengths are readily available.
1.4. Example:
Let's consider a triangle with sides a = 5 cm, b = 6 cm, and c = 7 cm.
-
Semi-perimeter (s): s = (5 + 6 + 7) / 2 = 9 cm
-
Heron's Formula: A = √[9(9-5)(9-6)(9-7)] = √[9 * 4 * 3 * 2] = √216 ≈ 14.7 cm²
This illustrates the ease and efficiency of Heron's formula.
Method 2: The ½absinC Formula – Direct and Efficient
This formula offers a remarkably elegant and direct approach to calculating the area:
A = ½ * a * b * sin C
Where:
- a and b are the lengths of two sides of the triangle.
- C is the angle between sides a and b.
This formula leverages the power of trigonometry. It's computationally efficient and doesn't require the intermediate step of finding the height.
2.1. Understanding the Derivation:
This formula is derived from the basic area formula (½ * base * height) by substituting the height with 'b * sin C'. This substitution stems directly from the definition of sine in a right-angled triangle formed by dropping a perpendicular from one vertex.
2.2. Example:
Consider a triangle with sides a = 8 cm, b = 10 cm, and the angle C between them is 30°.
A = ½ * 8 * 10 * sin 30° = 40 * 0.5 = 20 cm²
Method 3: Coordinate Geometry Approach – Using Vertices
If the coordinates of the vertices of a triangle are known, we can use the determinant method to calculate the area.
Let the vertices be A(x₁, y₁), B(x₂, y₂), and C(x₃, y₃). The area is given by:
A = ½ | (x₁(y₂ - y₃) + x₂(y₃ - y₁) + x₃(y₁ - y₂) ) |
The absolute value ensures a positive area.
3.1. Example:
Consider a triangle with vertices A(1, 2), B(4, 6), and C(7, 3).
A = ½ | (1(6 - 3) + 4(3 - 2) + 7(2 - 6)) | = ½ | (3 + 4 - 28) | = ½ | -21 | = 10.5 square units.
Choosing the Right Method: A Practical Guide
The best method depends on the information available:
-
If you know all three side lengths: Use Heron's formula. It's straightforward and computationally efficient.
-
If you know two sides and the included angle: Use the ½absinC formula. This is the most direct and efficient method in this scenario.
-
If you know the coordinates of the vertices: Employ the coordinate geometry approach. This is particularly useful when dealing with triangles in a coordinate system.
-
If you have other information, such as a combination of sides and angles: Use the Sine Rule combined with the basic area formula (½ * base * height) This approach offers flexibility when dealing with various types of available information.
Advanced Applications and Considerations: Beyond the Basics
The area of a non-right-angled triangle finds applications in various advanced contexts:
-
Calculus: Calculating areas under curves often involves breaking down the area into a series of small triangles.
-
Vector Geometry: The cross product of two vectors representing two sides of a triangle is directly related to its area.
-
Computer Graphics: Area calculations are fundamental in rendering algorithms, particularly for polygon filling and texture mapping.
-
Surveying and Land Measurement: Determining land areas involves frequently using triangle area calculations.
Conclusion: Mastering Area Calculation for Non-Right-Angled Triangles
Mastering the calculation of the area of non-right-angled triangles is a crucial skill for anyone working with geometry. By understanding the different methods – Heron's formula, the ½absinC formula, and the coordinate geometry approach – you equip yourself with versatile tools applicable to various situations and advanced applications. The choice of method depends on the specific information available, but each method provides a reliable path to accurately determining the area of any triangle, regardless of its shape or orientation. Regular practice and a firm grasp of the underlying principles will enhance your proficiency and enable you to confidently tackle complex geometric problems. Remember to choose the most efficient method based on the data provided to streamline your calculations and ensure accuracy.
Latest Posts
Latest Posts
-
Cuanto Equivale 32 Onzas En Litros
Mar 31, 2025
-
How Many Feet In 120 In
Mar 31, 2025
-
How Long Is 48 Inches In Cm
Mar 31, 2025
-
6 Is What Percent Of 7
Mar 31, 2025
-
How To Find Friction Without Coefficient
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about Area Of Non Right Angle Triangle . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
