Common Multiples Of 4 5 And 6
Kalali
Apr 05, 2025 · 6 min read
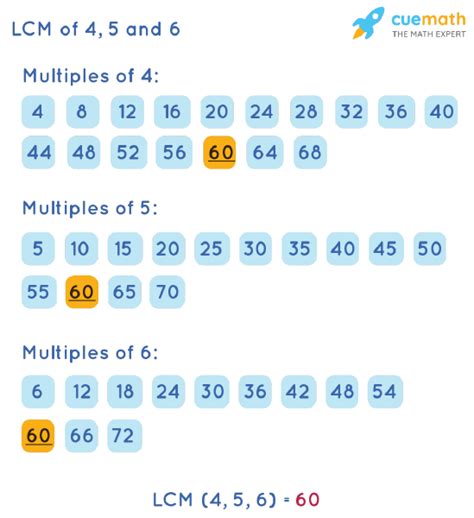
Table of Contents
Unveiling the Mysteries of Common Multiples: A Deep Dive into 4, 5, and 6
Finding common multiples, especially for a set of numbers like 4, 5, and 6, might seem daunting at first. However, understanding the underlying principles and employing a systematic approach can transform this seemingly complex task into a straightforward and even enjoyable mathematical exercise. This comprehensive guide will not only unravel the methods for finding the least common multiple (LCM) of 4, 5, and 6 but also explore broader concepts related to multiples and their applications.
Understanding Multiples
Before delving into the specifics of finding common multiples for 4, 5, and 6, let's solidify our understanding of the fundamental concept of multiples. A multiple of a number is the product of that number and any integer (whole number). For example:
- Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, and so on.
- Multiples of 5: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, and so on.
- Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, and so on.
Notice that these lists extend infinitely. Each number has an infinite number of multiples.
Identifying Common Multiples
A common multiple is a number that appears in the lists of multiples for two or more numbers. Looking at our examples above, we can already identify some common multiples of 4, 5, and 6:
- 60 appears in all three lists.
- 120 is also present in all three lists.
These are just two examples; there are infinitely many common multiples. The key is to find a systematic way to identify them, particularly the smallest one—the least common multiple (LCM).
Methods for Finding the Least Common Multiple (LCM)
There are several effective methods to determine the LCM of 4, 5, and 6. We'll explore two common approaches:
1. Listing Multiples
This method involves listing the multiples of each number until a common multiple is found. While straightforward for smaller numbers, it becomes less efficient as the numbers increase.
Let's list multiples for 4, 5, and 6:
- Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60, ...
- Multiples of 5: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, ...
- Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, ...
As we can see, the smallest common multiple among these lists is 60. Therefore, the LCM of 4, 5, and 6 is 60.
2. Prime Factorization Method
This method is significantly more efficient, particularly for larger numbers. It involves breaking down each number into its prime factors.
- Prime factorization of 4: 2 x 2 = 2²
- Prime factorization of 5: 5 (5 is a prime number)
- Prime factorization of 6: 2 x 3
To find the LCM, we take the highest power of each prime factor present in the factorizations:
- The highest power of 2 is 2².
- The highest power of 3 is 3.
- The highest power of 5 is 5.
Multiplying these together gives us: 2² x 3 x 5 = 4 x 3 x 5 = 60.
Therefore, the LCM of 4, 5, and 6 using prime factorization is also 60.
Why the LCM is Important
Understanding and calculating the LCM is crucial in various mathematical contexts and real-world applications:
-
Fraction Operations: Finding a common denominator when adding or subtracting fractions requires finding the LCM of the denominators. For example, to add 1/4 and 1/6, we need to find the LCM of 4 and 6 (which is 12), converting the fractions to 3/12 and 2/12 respectively.
-
Scheduling and Timing: The LCM is useful in solving problems involving cyclical events. Imagine three machines that operate on cycles of 4, 5, and 6 hours respectively. The LCM (60) represents the time it takes for all three machines to complete a full cycle simultaneously.
-
Measurement and Conversions: The LCM plays a role in unit conversions and finding compatible measurements.
-
Abstract Algebra: The concept extends into higher-level mathematics, particularly in abstract algebra and number theory.
Exploring Further: Beyond the LCM
While the LCM is the smallest common multiple, there are infinitely many others. These can be found by multiplying the LCM by any positive integer. For example, multiples of the LCM (60) are also common multiples of 4, 5, and 6:
- 60 x 2 = 120
- 60 x 3 = 180
- 60 x 4 = 240
- and so on...
Practical Applications and Examples
Let's illustrate the practical application of finding common multiples with some real-world scenarios:
Scenario 1: The Baker's Dilemma
A baker makes loaves of bread in batches of 4, cakes in batches of 5, and pastries in batches of 6. What is the smallest number of batches of each item the baker needs to make to have an equal number of each?
Solution: This problem requires finding the LCM of 4, 5, and 6, which we've established is 60. This means the baker needs to make 15 batches of bread (60/4), 12 batches of cakes (60/5), and 10 batches of pastries (60/6) to have an equal number of each item.
Scenario 2: The Synchronized Clocks
Three clocks chime at intervals of 4, 5, and 6 seconds respectively. When will they all chime together again after simultaneously chiming at the start?
Solution: To find when the clocks will chime together, we need to find the LCM of 4, 5, and 6, which is 60. They will chime together again after 60 seconds.
Scenario 3: The Tile Problem
You need to tile a rectangular floor using square tiles. The dimensions of the floor are 120 cm by 150 cm. What is the largest possible size of a square tile that will fit perfectly without any cutting or gaps?
Solution: To solve this, we need to find the greatest common divisor (GCD) of 120 and 150. The GCD represents the largest square tile that will fit perfectly. We can use the Euclidean algorithm or prime factorization to find the GCD. However, for the purposes of this section focusing on LCM, we'll note that the problem highlights the relationship between LCM and GCD. The product of the LCM and GCD of two numbers is always equal to the product of the two numbers.
Conclusion
Finding the common multiples, and particularly the least common multiple, of numbers like 4, 5, and 6 may initially appear complex, but with a systematic approach and understanding of the underlying principles, it becomes a manageable and valuable mathematical skill. Whether using the listing method or the more efficient prime factorization method, the process provides a pathway to solving problems in diverse fields, from baking to scheduling and beyond. The applications extend far beyond the initial problem, offering a gateway to a deeper appreciation of mathematical concepts and their real-world significance. Remember, practice makes perfect, so continue exploring different sets of numbers and applying these techniques to solidify your understanding.
Latest Posts
Latest Posts
-
How To Convert Moles To Mass
Apr 06, 2025
-
Cross Sections Of A Rectangular Prism
Apr 06, 2025
-
How Much Is 150ml In Cups
Apr 06, 2025
-
4 To The Power Of 9
Apr 06, 2025
-
How Big Is 22cm In Inches
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about Common Multiples Of 4 5 And 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
