Cross Sections Of A Rectangular Prism
Kalali
Apr 06, 2025 · 6 min read
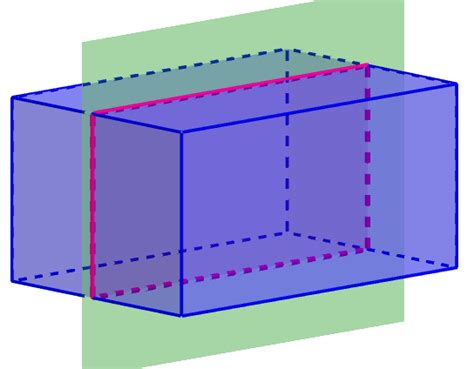
Table of Contents
Cross Sections of a Rectangular Prism: A Comprehensive Guide
Understanding the cross sections of a three-dimensional shape is crucial in various fields, from architecture and engineering to advanced mathematics. This comprehensive guide delves into the fascinating world of cross sections, specifically focusing on the rectangular prism. We'll explore different types of cross sections, how they're formed, and the geometric properties they exhibit. By the end, you'll have a solid grasp of this fundamental concept and be able to visualize and predict the shapes resulting from various slicing techniques.
What is a Cross Section?
A cross section is the two-dimensional shape that emerges when a three-dimensional object is sliced through by a plane. Imagine a perfectly sharp knife cutting through a solid; the resulting surface of the cut is the cross section. The shape and properties of the cross section depend entirely on the orientation of the slicing plane relative to the original object. In the case of a rectangular prism, the possibilities are surprisingly diverse.
The Rectangular Prism: A Foundation for Exploration
A rectangular prism, also known as a rectangular parallelepiped or cuboid, is a three-dimensional object with six rectangular faces. Each face is parallel to its opposite face, and all angles are right angles (90 degrees). Its defining characteristics—its straight edges and right angles—make it an ideal shape for exploring cross sections. The predictability of its geometry allows us to easily predict the resulting two-dimensional shapes from various cuts.
Exploring Different Cross Sections of a Rectangular Prism
The beauty of exploring cross sections of a rectangular prism lies in the variety of shapes that can be created by simply changing the orientation of the cutting plane. Let's delve into some examples:
1. Rectangular Cross Sections: The Simplest Case
When the cutting plane is parallel to any of the faces of the rectangular prism, the resulting cross section is a rectangle. This is the most straightforward case. The dimensions of the rectangle will depend on the location and orientation of the cutting plane relative to the prism's dimensions. If the plane is parallel to and exactly halfway between two opposite faces, the resulting rectangle will be congruent to those faces.
2. Square Cross Sections: A Special Case of Rectangles
If the rectangular prism is actually a cube (all sides are equal), any cross section parallel to a face will yield a square. In a non-cubic rectangular prism, a square cross section is only possible under specific conditions related to the prism's dimensions and the angle of the cutting plane.
3. Triangular Cross Sections: Introducing Angles
By tilting the cutting plane, we introduce angles and can create triangles. These triangles will be formed by the intersection of the plane with three of the prism's faces. The type of triangle (equilateral, isosceles, scalene) will depend on the angle and position of the plane. To obtain an equilateral triangle, you would need a very specific, carefully calculated angle and position of the cutting plane relative to the prism.
4. Trapezoidal Cross Sections: Parallel Sides, Tilted Plane
A trapezoid (also known as a trapezium) is a quadrilateral with at least one pair of parallel sides. A trapezoidal cross section can be created by cutting through the rectangular prism with a plane that's not parallel to any of its faces but intersects at least two pairs of opposite faces. The parallelism of the trapezoid's bases is a direct result of the parallelism of the opposite faces of the prism. The other two sides of the trapezoid will be formed by the plane's intersection with the remaining faces.
5. Parallelogram Cross Sections: More than one pair of parallel sides
A parallelogram is a quadrilateral with two pairs of parallel sides. In a rectangular prism, a parallelogram cross section is produced if the cutting plane is tilted such that it intersects the prism in a way that creates two pairs of parallel lines. This is a more general case than the trapezoid, where only one pair of sides is necessarily parallel.
6. Pentagonal Cross Sections: Five-Sided Figures
It's possible to create a pentagonal cross section by carefully positioning and angling the cutting plane. This requires the plane to intersect five faces of the rectangular prism. This type of cross section is less common compared to the rectangular, triangular, and trapezoidal sections. The specific dimensions of the pentagon will depend critically on the precise angle of the cut.
7. Hexagonal Cross Sections: The Most Complex Case
The most complex cross section obtainable from a rectangular prism is a hexagon. This is achieved by angling the plane such that it intersects all six faces of the prism. This type of cross-section requires a very specific orientation of the cutting plane; otherwise, you'd get a pentagon or a lower number of sides. The resulting hexagon will generally be irregular, meaning its sides and angles will not be equal.
Predicting Cross Section Shapes: A Systematic Approach
Predicting the shape of a cross section involves visualizing the intersection of the cutting plane with the edges and faces of the rectangular prism. Consider the following steps:
- Visualize the Plane: Imagine the plane slicing through the prism.
- Identify Intersection Points: Determine where the plane intersects the edges of the prism.
- Connect the Points: Connect the intersection points to form the cross section.
- Analyze the Shape: Classify the resulting shape based on its properties (number of sides, parallel sides, angles).
Applications of Understanding Cross Sections
The knowledge of cross sections has wide-ranging applications across diverse fields:
- Engineering: In structural engineering, understanding cross sections helps in determining the strength and stability of beams and other structural elements.
- Architecture: Architects use cross-sectional drawings to visualize the internal structure and design of buildings.
- Computer-aided design (CAD): Cross sections are fundamental in 3D modeling and design software.
- Geology: Geologists use cross sections to study the subsurface structure of the Earth.
- Mathematics: The concept of cross sections is essential in integral calculus and other advanced mathematical concepts.
Beyond Rectangular Prisms: Expanding the Concept
The principles discussed here for rectangular prisms can be applied to other three-dimensional shapes as well. While the specific shapes of cross sections will vary, the underlying concept of intersecting a plane with a solid to create a two-dimensional figure remains consistent. Exploring cross sections of other shapes, such as pyramids, cylinders, cones, and spheres, reveals a rich tapestry of geometric possibilities.
Conclusion: A Deeper Appreciation of Geometry
Understanding cross sections, especially those of a rectangular prism, provides a deeper appreciation for the relationship between two-dimensional and three-dimensional geometry. The ability to visualize and predict cross-sectional shapes is a valuable skill in many fields, from engineering and architecture to advanced mathematics. This comprehensive guide has armed you with the knowledge and tools to confidently tackle the complexities of cross sections, allowing you to further explore the fascinating world of geometry. Remember, practice is key! Try visualizing different cutting planes and predicting the resulting shapes – you'll soon develop an intuitive understanding of this fundamental geometric concept.
Latest Posts
Latest Posts
-
What Is A Standard Form Of A Polynomial
Apr 08, 2025
-
Does This Graph Show A Function Explain How You Know
Apr 08, 2025
-
What Is 75 Percent Of 15
Apr 08, 2025
-
How Many Grams Is 3000 Milligrams
Apr 08, 2025
-
Is Luster A Chemical Or Physical Property
Apr 08, 2025
Related Post
Thank you for visiting our website which covers about Cross Sections Of A Rectangular Prism . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.