Coordination Number In Simple Cubic Crystal Structure
Kalali
Mar 27, 2025 · 6 min read
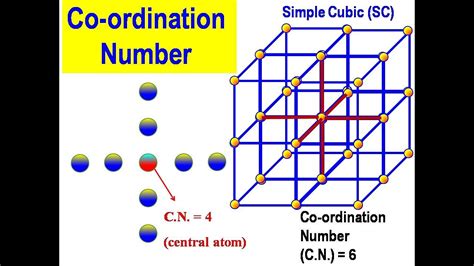
Table of Contents
Coordination Number in Simple Cubic Crystal Structure: A Comprehensive Guide
The simple cubic (SC) crystal structure, while the simplest to visualize, offers valuable insights into fundamental concepts in crystallography, particularly the concept of coordination number. Understanding coordination number is crucial for predicting material properties and behaviors. This article delves deep into the coordination number within the SC structure, exploring its calculation, significance, and implications for material science.
What is a Coordination Number?
In crystallography, the coordination number refers to the number of nearest-neighbor atoms surrounding a central atom in a crystal lattice. This number directly reflects the bonding environment of the atom and significantly influences the crystal's overall properties, including density, hardness, and electrical conductivity. It's a fundamental parameter in defining the crystal structure and its related characteristics. Think of it as a measure of how many immediate "friends" an atom has in the crystal.
Determining the Coordination Number in a Simple Cubic Structure
The simple cubic structure is characterized by atoms positioned only at the corners of a cube. This arrangement leads to a relatively low coordination number compared to more complex structures. To determine this number, let's visualize a single atom within the SC lattice:
Visualizing the Nearest Neighbors
Imagine an atom nestled at the corner of a cube. Its nearest neighbors are the atoms directly touching it. Looking carefully, we can see that these neighbors are located at the corners of the cube adjacent to the central atom.
Counting the Nearest Neighbors
Each of the six faces of the cube shares an atom with the central atom. Therefore, each central atom is directly surrounded by six nearest neighbors. This direct count provides the coordination number.
Therefore, the coordination number for a simple cubic crystal structure is 6.
Implications of a Coordination Number of 6
The coordination number of 6 in the simple cubic structure has several key implications:
-
Low Packing Efficiency: The SC structure has a relatively low atomic packing factor (APF) – only 52%. This means that a significant amount of space within the unit cell is empty. This low packing density impacts the material's physical properties, resulting in a lower density compared to other crystal structures with higher coordination numbers.
-
Lower Density: Because of the inefficient packing, materials crystallizing in the SC structure tend to be less dense than those with face-centered cubic (FCC) or body-centered cubic (BCC) structures.
-
Mechanical Properties: The lower coordination number contributes to lower mechanical strength and hardness. The atoms are not as tightly bound to their neighbors as in structures with higher coordination numbers. This lack of robust interatomic bonding leads to increased susceptibility to deformation.
-
Electrical Conductivity: The SC structure's influence on electrical conductivity is complex and depends on other factors such as the type of atom involved and the presence of defects. However, in general, the relatively weaker bonding in SC structures could potentially affect electron mobility and thus the overall conductivity.
-
Limited Occurrence: Due to its low packing efficiency and less favorable energy state, the simple cubic structure is relatively rare in nature. Many elements and compounds prefer more closely packed structures like FCC or BCC to minimize their energy. Most naturally occurring materials adopt crystal structures with higher coordination numbers, leading to greater stability.
Contrasting Coordination Numbers Across Crystal Structures
To highlight the significance of coordination number in the SC structure, let's compare it to other common crystal structures:
-
Body-Centered Cubic (BCC): In a BCC structure, each atom is surrounded by eight nearest neighbors located at the corners of a cube, along with one atom at the center of the cube. The coordination number for BCC is 8. This leads to a higher packing efficiency (68%) and generally stronger, denser materials.
-
Face-Centered Cubic (FCC): The FCC structure boasts a coordination number of 12. Each atom is surrounded by twelve nearest neighbors, resulting in the highest packing efficiency (74%) among the three common cubic structures. FCC structures are generally associated with high ductility, malleability, and high density.
-
Hexagonal Close-Packed (HCP): This non-cubic structure also exhibits a coordination number of 12, like FCC. The high packing efficiency (74%) leads to similar properties as FCC structures, but with slightly different anisotropy (direction-dependent properties).
Advanced Concepts and Applications
The concept of coordination number extends beyond the simple identification of nearest neighbors. More nuanced considerations include:
-
Second Nearest Neighbors: While coordination number primarily focuses on nearest neighbors, considering second (and even further) nearest neighbors offers a more complete picture of atomic interactions. The distance to these neighbors and the nature of the interaction significantly influence material properties.
-
Coordination Polyhedra: Visualizing the coordination environment by drawing a polyhedron (geometric shape) connecting the central atom to its nearest neighbors is a powerful tool for understanding bonding geometries and interactions. The shape and characteristics of the coordination polyhedron reflect the symmetry and bond angles within the crystal structure.
-
Defects and Imperfections: Real crystals are not perfect; they contain defects like vacancies, interstitials, and dislocations. These defects disrupt the regular arrangement of atoms, locally altering the coordination number and influencing overall material properties. Understanding the interplay between coordination number and crystal defects is crucial in materials science.
Applications of Coordination Number in Materials Science
The concept of coordination number has far-reaching applications in various fields of material science, including:
-
Predicting Material Properties: Knowledge of coordination number helps predict a material's mechanical properties (strength, hardness, ductility), density, and thermal and electrical conductivity.
-
Alloy Design: By understanding how coordination number affects the bonding characteristics and interaction between different atomic species, materials scientists can effectively design alloys with desired properties.
-
Catalysis: Coordination number plays a critical role in catalytic activity. The active sites on a catalyst often exhibit specific coordination environments that influence their ability to bind reactants and promote chemical reactions.
-
Nanomaterials: In the realm of nanomaterials, precise control over coordination number is essential for tailoring material properties. By controlling synthesis parameters, scientists can create nanostructures with specific coordination environments that exhibit unique optical, electrical, or magnetic characteristics.
-
Geochemistry: Coordination number is used in geochemistry to understand mineral structures, compositions, and chemical bonding. It provides essential knowledge of how elements are coordinated in minerals, influencing their behavior in geological processes.
Conclusion: Coordination Number – A Cornerstone of Crystallography
The coordination number, a seemingly simple concept, offers a profound understanding of the structure and properties of crystalline materials. The simple cubic crystal structure, with its coordination number of 6, serves as a fundamental example to illustrate this principle. By contrasting this with other crystal structures, we highlight the significant impact of coordination number on various material characteristics. Its application extends far beyond basic crystallography, playing a vital role in many areas of materials science, from predicting properties to designing new materials with tailored functionalities. A solid grasp of coordination number is essential for anyone working in material science, chemistry, and related fields. This comprehensive overview hopefully provides a solid foundation for further exploration of this essential crystallographic concept.
Latest Posts
Latest Posts
-
What Percentage Is 11 Out Of 20
Mar 30, 2025
-
Cuanto Es 2 Kilos En Libras
Mar 30, 2025
-
3 Is What Percent Of 8
Mar 30, 2025
-
What Percent Of 20 Is 50
Mar 30, 2025
-
How Does A Sedimentary Rock Become An Igneous Rock
Mar 30, 2025
Related Post
Thank you for visiting our website which covers about Coordination Number In Simple Cubic Crystal Structure . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
