Cross Section Of A Rectangular Pyramid
Kalali
Apr 02, 2025 · 6 min read
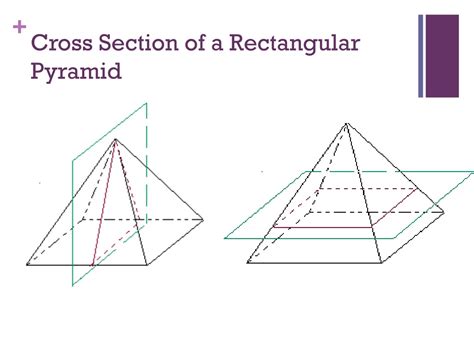
Table of Contents
Unveiling the Mysteries: A Deep Dive into the Cross-Section of a Rectangular Pyramid
Understanding the intricacies of three-dimensional shapes is crucial in various fields, from architecture and engineering to computer graphics and game design. Among these shapes, the rectangular pyramid holds a unique position, offering a fascinating exploration of geometry and spatial reasoning. This article delves deep into the concept of a cross-section of a rectangular pyramid, exploring its various forms, properties, and applications. We will move beyond simple definitions and uncover the mathematical elegance hidden within this seemingly straightforward geometric object.
What is a Cross-Section?
Before we embark on our journey into the cross-section of a rectangular pyramid, let's establish a clear understanding of the term "cross-section." A cross-section is essentially the shape you get when you slice through a three-dimensional object with a plane. Imagine a perfectly sharp knife cutting through a solid; the resulting surface of the cut is the cross-section. The shape and characteristics of this cross-section depend entirely on the orientation of the cutting plane relative to the object's structure.
Exploring Different Cross-Sections of a Rectangular Pyramid
A rectangular pyramid, characterized by its rectangular base and four triangular faces meeting at a single apex, can produce a variety of cross-sections depending on how it is intersected by a plane. Let's explore some key possibilities:
1. Cross-Sections Parallel to the Base:
When a plane cuts a rectangular pyramid parallel to its base, the resulting cross-section is always similar to the base itself. This means the cross-section will be a rectangle, sharing the same proportions as the base but with smaller dimensions. The size of this rectangular cross-section varies linearly with its distance from the apex. The closer the plane is to the apex, the smaller the rectangle; the closer it is to the base, the larger the rectangle, until it becomes identical to the base itself. This property is fundamental to understanding the scaling and proportional relationships within the pyramid.
2. Cross-Sections Perpendicular to the Base and Passing Through the Apex:
Cutting the pyramid with a plane perpendicular to its base and passing through the apex creates a triangular cross-section. Specifically, this will be an isosceles triangle if the cutting plane passes through the midpoint of opposite sides of the rectangular base. The dimensions of this triangle will depend on the exact orientation of the plane. Different orientations will result in different triangles, but they will always share the apex of the pyramid. This type of cross-section elegantly highlights the relationship between the apex and the base of the pyramid.
3. Cross-Sections Perpendicular to the Base and Not Passing Through the Apex:
This scenario introduces more complexity. The cross-section produced will be a trapezoid. The trapezoid's shape and dimensions will be highly dependent on the specific location and orientation of the cutting plane. The properties of this trapezoid, such as its base lengths and height, can be calculated using geometry principles, but the calculations can become significantly more involved. This scenario exemplifies the richness of geometrical possibilities inherent in even relatively simple 3D shapes.
4. Cross-Sections at Oblique Angles:
The most general case involves cutting the pyramid with a plane at an oblique angle – not parallel or perpendicular to the base. In this case, the cross-section can take on a variety of shapes, often irregular quadrilaterals. Determining the exact shape and dimensions of such cross-sections requires more advanced techniques in three-dimensional geometry, possibly involving vector analysis and linear algebra. These complex cross-sections highlight the versatility and unpredictable nature of plane intersections with three-dimensional objects.
Mathematical Derivations and Applications
The concept of cross-sections isn't merely an abstract geometric exercise; it has significant practical applications:
-
Volume Calculation: Understanding cross-sections is fundamental to calculating the volume of a rectangular pyramid using integral calculus. By integrating the area of infinitesimally thin cross-sections along the height of the pyramid, we can precisely determine its volume. This method showcases the power of combining geometry and calculus.
-
Engineering and Architecture: In engineering and architectural design, cross-sections are crucial for analyzing the strength and stability of structures. Understanding how a plane intersects a pyramid-shaped structure (or any three-dimensional structure) allows engineers to assess its stress distribution and ensure structural integrity. For example, analyzing the cross-sections of a pyramid-shaped roof helps determine the necessary structural support.
-
Computer-Aided Design (CAD): CAD software extensively uses cross-section analysis. When designing three-dimensional models, engineers and designers frequently need to visualize the internal structure of their creations. Generating cross-sections allows for a detailed understanding of the object’s internal composition and helps in detecting potential design flaws.
-
Geology and Earth Sciences: In geology, analyzing cross-sections of geological formations is vital for understanding the subsurface structure of the Earth. Cross-sections of rock strata reveal the history of geological processes, aiding in mineral exploration and understanding tectonic activity.
Advanced Concepts and Further Exploration
The exploration of rectangular pyramid cross-sections can be extended to even more complex scenarios:
-
Multiple Cross-Sections: Consider the implications of intersecting a rectangular pyramid with multiple planes simultaneously. This could lead to intricate and fascinating geometric arrangements.
-
Non-planar Cross-Sections: While we have focused on plane cross-sections, the concept could be extended to non-planar surfaces, which would introduce significant mathematical challenges and require more advanced techniques.
-
Relationship to other Geometric Shapes: Exploring the relationship between the cross-sections of a rectangular pyramid and other geometric shapes, such as prisms and cones, could provide valuable insights into geometrical relationships.
Conclusion: A Deeper Appreciation of Geometry
The cross-section of a rectangular pyramid, initially seemingly straightforward, unveils a rich tapestry of geometric possibilities. From simple rectangles and triangles to complex irregular quadrilaterals, the diversity of cross-sections reflects the inherent complexity and beauty of three-dimensional shapes. Understanding these cross-sections is not just an academic pursuit; it underpins crucial applications in various fields, highlighting the vital role of geometry in our world. This exploration serves as a testament to the enduring power and elegance of geometrical principles and their far-reaching impact on our understanding of the physical world. By delving into the cross-sections of a rectangular pyramid, we gain a deeper appreciation for the intricate relationships between geometry, calculus, and the real-world applications that arise from their interaction. Continued investigation into these topics will undoubtedly uncover even more fascinating and insightful discoveries.
Latest Posts
Latest Posts
-
How Many Hours Is 125 Minutes
Apr 03, 2025
-
4 To The Power Of 12
Apr 03, 2025
-
What Are The Disadvantages Of Sexual Reproduction
Apr 03, 2025
-
How Many Inches Is 210 Cm
Apr 03, 2025
-
What Is 11 4 As A Decimal
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Cross Section Of A Rectangular Pyramid . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
