Cuál Es El Valor Absoluto De -3
Kalali
Apr 05, 2025 · 5 min read
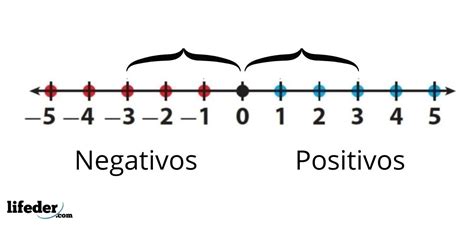
Table of Contents
What is the Absolute Value of -3? A Deep Dive into Absolute Value
The seemingly simple question, "What is the absolute value of -3?", opens a door to a fascinating exploration of a fundamental mathematical concept. While the answer itself is straightforward – 3 – understanding the why behind it requires delving into the definition, properties, and applications of absolute value. This comprehensive guide will explore absolute value in detail, providing a clear and insightful understanding beyond just the numerical result.
Understanding Absolute Value: The Distance Analogy
The absolute value of a number is its distance from zero on the number line. This is a crucial conceptualization because it emphasizes the magnitude of the number, ignoring its sign (positive or negative). Think of it like this: if you're 3 miles from your house, it doesn't matter whether you're 3 miles north or 3 miles south; the distance remains 3 miles. Similarly, the absolute value of both 3 and -3 is 3 because both are 3 units away from zero.
Key takeaway: Absolute value is always non-negative. It represents magnitude, not direction.
Notation and Definition
The absolute value of a number x is denoted by |x|. Formally, the definition is as follows:
- If x ≥ 0, then |x| = x (The absolute value of a non-negative number is the number itself.)
- If x < 0, then |x| = -x (The absolute value of a negative number is its opposite.)
Let's illustrate with examples:
- |5| = 5
- |-5| = -(-5) = 5
- |0| = 0
- |-3| = -(-3) = 3 (This directly answers our initial question!)
Properties of Absolute Value
Understanding the properties of absolute value is essential for manipulating expressions and solving equations involving absolute value. These properties are:
- Non-negativity: |x| ≥ 0 for all real numbers x.
- Identity property: |x| = 0 if and only if x = 0.
- Even property: |-x| = |x| for all real numbers x. The absolute value of a number and its opposite are equal.
- Multiplication property: |xy| = |x| |y| for all real numbers x and y. The absolute value of a product is the product of the absolute values.
- Division property: |x/y| = |x|/|y| for all real numbers x and y, where y ≠ 0. The absolute value of a quotient is the quotient of the absolute values.
- Triangle inequality: |x + y| ≤ |x| + |y| for all real numbers x and y. The absolute value of a sum is less than or equal to the sum of the absolute values.
Solving Equations and Inequalities Involving Absolute Value
Absolute value often appears in equations and inequalities. Solving these requires careful consideration of the definition. For example, consider the equation |x| = 5. This means that x is 5 units away from zero, so x can be either 5 or -5.
Solving inequalities is slightly more complex. For example, consider |x| < 5. This inequality means that x is less than 5 units away from zero. This translates to -5 < x < 5. In contrast, |x| > 5 means x is more than 5 units away from zero, so x < -5 or x > 5.
Absolute Value in Geometry and Other Applications
Beyond its algebraic use, absolute value has significant geometric interpretations. As mentioned earlier, it represents distance. The distance between two points on the number line, a and b, is given by |a - b|. This concept extends to higher dimensions as well, where absolute value plays a crucial role in defining distance in more complex spaces.
Furthermore, absolute value finds applications in various fields:
- Physics: Absolute value is used to represent magnitude without direction, such as speed (as opposed to velocity, which includes direction).
- Computer Science: Absolute value is essential in algorithms related to distance calculations, sorting, and error analysis.
- Engineering: Absolute value helps in analyzing magnitudes of forces, stresses, and other physical quantities.
- Statistics: Absolute deviation, which is based on absolute value, is a measure of variability in data.
Advanced Concepts: Absolute Value Function and Graph
The absolute value can be formally defined as a piecewise function:
f(x) = |x| = { x, if x ≥ 0; -x, if x < 0 }
The graph of this function is a V-shaped curve with its vertex at the origin (0,0). The right branch is the line y = x, and the left branch is the line y = -x. The function is continuous but not differentiable at x = 0 (the vertex).
Misconceptions about Absolute Value
Several common misconceptions surround absolute value:
- Absolute value is not distributive: |x + y| ≠ |x| + |y| in general. The triangle inequality states |x + y| ≤ |x| + |y|. Equality holds only when x and y have the same sign or one of them is zero.
- Absolute value does not simply remove the negative sign: While | -3 | = 3, the process is not merely "removing the negative sign". It's about finding the distance from zero. This distinction is crucial for understanding the operations involving absolute value.
- Absolute value is not the same as squaring: While both |x| and x² are always non-negative, they are not equivalent for negative x. For example, |-3| = 3, while (-3)² = 9.
Conclusion: Mastering the Absolute Value Concept
The absolute value of -3, simply 3, is more than just a numerical answer. It's a gateway to a deeper understanding of a fundamental mathematical concept with far-reaching implications. By understanding its definition, properties, applications, and common misconceptions, you can confidently approach and solve problems involving absolute value in various mathematical contexts and real-world scenarios. This comprehensive exploration aimed to equip you not only with the solution to the initial question but also with a robust understanding of the absolute value concept, its uses, and its nuances. Remember that a solid grasp of absolute value forms a crucial foundation for more advanced mathematical topics.
Latest Posts
Latest Posts
-
What Percent Is 2 Of 6
Apr 06, 2025
-
Convert 12 Degrees Celsius To Fahrenheit
Apr 06, 2025
-
Aluminum Foil Mixture Or Pure Substance
Apr 06, 2025
-
Cual Es El 20 De 20
Apr 06, 2025
-
What Is The Difference Between Community And Population
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about Cuál Es El Valor Absoluto De -3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
