What Percent Is 2 Of 6
Kalali
Apr 06, 2025 · 4 min read
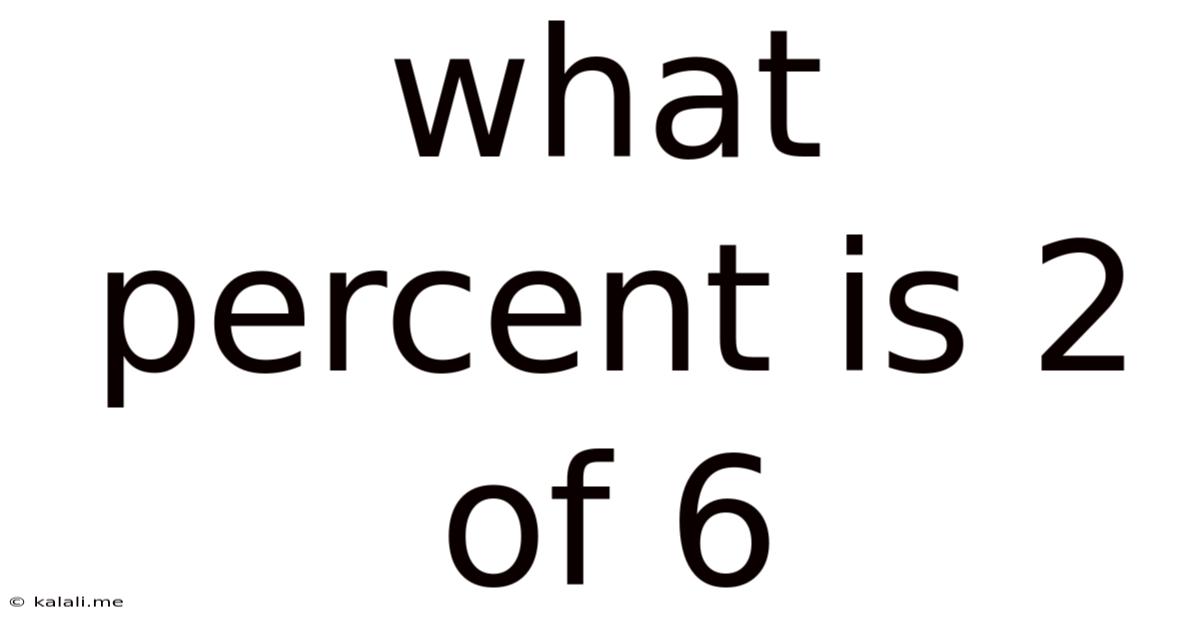
Table of Contents
What Percent is 2 of 6? A Deep Dive into Percentage Calculations
Understanding percentages is a fundamental skill in numerous aspects of life, from calculating discounts and tax to analyzing data and understanding financial reports. This article will delve into the seemingly simple question, "What percent is 2 of 6?", exploring the calculation process, different approaches to solving it, and extending the concept to broader applications. We'll also cover related percentage problems and offer practical examples to solidify your understanding.
Calculating the Percentage: The Fundamental Approach
The core of percentage calculation lies in understanding the relationship between a part and a whole. In our example, "2 of 6," 2 represents the part and 6 represents the whole. To find the percentage, we follow these steps:
-
Formulate the Ratio: Express the relationship between the part and the whole as a fraction: 2/6.
-
Convert the Fraction to a Decimal: Divide the numerator (2) by the denominator (6): 2 ÷ 6 = 0.333... (This is a repeating decimal).
-
Convert the Decimal to a Percentage: Multiply the decimal by 100: 0.333... × 100 = 33.33...%
Therefore, 2 is approximately 33.33% of 6. The "..." indicates the repeating decimal, which can be rounded to a suitable level of precision depending on the context. For most practical purposes, rounding to two decimal places (33.33%) is sufficient.
Alternative Methods and Simplification
While the above method is straightforward, there are alternative approaches that can simplify the calculation, especially with more complex problems.
Simplifying the Fraction
Before converting to a decimal, simplifying the fraction can make the calculation easier. In our case, both 2 and 6 are divisible by 2:
2/6 = 1/3
Now, converting 1/3 to a decimal: 1 ÷ 3 = 0.333...
Multiplying by 100 gives us the same result: 0.333... × 100 = 33.33...%
This method demonstrates that simplifying the fraction first can streamline the calculation process, particularly when dealing with larger numbers.
Using Proportions
Another approach involves setting up a proportion:
Part/Whole = Percentage/100
Substituting our values:
2/6 = x/100
To solve for x (the percentage), cross-multiply:
6x = 200
x = 200/6 = 33.33...%
Expanding the Concept: Applications and Variations
The fundamental principle of calculating percentages—finding the ratio of a part to a whole and expressing it as a percentage—extends to a wide range of applications:
Percentage Increase and Decrease
Imagine a scenario where a product initially costs $6 and its price increases by $2. To calculate the percentage increase:
-
Find the difference: $2 (increase)
-
Express the difference as a fraction of the original price: $2/$6 = 1/3
-
Convert to a percentage: (1/3) × 100 = 33.33%
The price increased by 33.33%. Similarly, percentage decreases can be calculated using the same principles, substituting the decrease amount for the increase.
Finding the Whole Given a Percentage and Part
Let's say you know that 33.33% of a certain number is 2. How do you find the original number (the whole)?
-
Convert the percentage to a decimal: 33.33% = 0.333...
-
Set up an equation: 0.333... × x = 2 (where x is the whole)
-
Solve for x: x = 2 / 0.333... = 6
This demonstrates the reverse calculation, where you can determine the whole given a part and its corresponding percentage.
Percentage of a Percentage
Calculating the percentage of a percentage is another common application. For example, finding 20% of 33.33% of 6:
-
Calculate 33.33% of 6: 0.333... × 6 = 2
-
Calculate 20% of 2: 0.20 × 2 = 0.4
Therefore, 20% of 33.33% of 6 is 0.4.
Real-World Examples and Practical Applications
The ability to calculate percentages is crucial in various real-world scenarios:
-
Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns.
-
Retail: Determining sale prices, calculating markups, and analyzing sales data.
-
Statistics: Interpreting survey results, analyzing data sets, and understanding probability.
-
Science: Expressing experimental results, calculating error margins, and analyzing data trends.
Conclusion: Mastering Percentage Calculations
Understanding how to calculate percentages, even seemingly simple ones like "What percent is 2 of 6?", is essential for navigating numerous aspects of daily life and professional endeavors. Through the various methods outlined in this article—the fundamental approach, simplification of fractions, using proportions—you can build a solid foundation in percentage calculations. Remember to always consider the context and round your answers appropriately for clarity and practical application. By mastering this fundamental mathematical concept, you'll be better equipped to tackle complex problems and make informed decisions in various fields. The ability to interpret and utilize percentage calculations efficiently is a valuable skill that enhances analytical thinking and problem-solving abilities.
Latest Posts
Latest Posts
-
Who And When Was Carbon Discovered
Apr 07, 2025
-
A Substance That Combines With Hydrogen Ions
Apr 07, 2025
-
How Many Inches In 71 Cm
Apr 07, 2025
-
How Many Feet Are In 126 Inches
Apr 07, 2025
-
How Tall Is 143 Cm In Feet
Apr 07, 2025
Related Post
Thank you for visiting our website which covers about What Percent Is 2 Of 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.