Diagonals Of Rhombus Bisect Vertex Angles
Kalali
Apr 05, 2025 · 5 min read
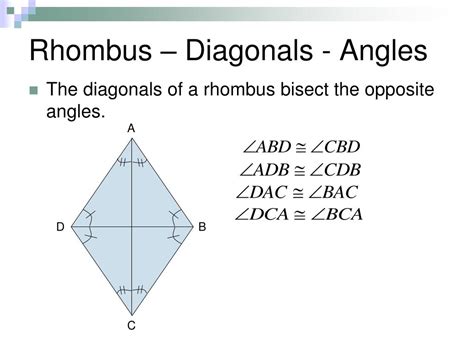
Table of Contents
Diagonals of a Rhombus Bisect Vertex Angles: A Comprehensive Exploration
The rhombus, a captivating quadrilateral with all sides equal in length, holds a unique geometric property: its diagonals bisect the vertex angles. This seemingly simple statement underpins a wealth of mathematical concepts and practical applications. This article delves deep into this property, exploring its proof, implications, and applications across various mathematical fields. We will examine the relationship between rhombuses, squares, and other quadrilaterals, highlighting the distinctive characteristics that set the rhombus apart.
Understanding the Fundamentals: Rhombuses and Their Properties
Before diving into the proof of our central theorem, let's establish a solid foundation by defining a rhombus and reviewing its key properties. A rhombus is a quadrilateral with all four sides congruent (equal in length). This simple definition leads to a host of other important characteristics:
- Opposite sides are parallel: This stems directly from the equal side lengths and the definition of a parallelogram. Parallel lines are equidistant throughout their length.
- Opposite angles are equal: A direct consequence of the parallel sides. When parallel lines are intersected by a transversal, alternate interior angles are congruent.
- Consecutive angles are supplementary: The sum of any two consecutive angles equals 180 degrees. This is because consecutive angles form a linear pair.
- Diagonals bisect each other: The diagonals intersect at a point that divides each diagonal into two equal segments. This is a common characteristic of parallelograms, and a rhombus is a type of parallelogram.
It is crucial to understand these properties before we tackle the core topic: how the diagonals bisect the vertex angles. These fundamental characteristics form the building blocks for our subsequent proofs and analyses. These properties aren't just theoretical; they find practical use in various fields like architecture, engineering, and computer graphics.
The Proof: Diagonals Bisect Vertex Angles
Now, let's tackle the central claim: the diagonals of a rhombus bisect its vertex angles. We'll demonstrate this using a combination of geometric principles and logical reasoning.
Theorem: The diagonals of a rhombus bisect its vertex angles.
Proof:
Consider a rhombus ABCD, with diagonals AC and BD intersecting at point O.
-
Congruent Triangles: We begin by focusing on triangles ΔAOB and ΔAOD. Since all sides of the rhombus are equal (AB = BC = CD = DA), and the diagonals bisect each other (AO = OC and BO = OD), we can use the SSS (Side-Side-Side) congruence postulate. Specifically:
- AB = AD (sides of a rhombus)
- AO = AO (common side)
- BO = OD (diagonals bisect each other)
Therefore, ΔAOB ≅ ΔAOD (SSS congruence).
-
Congruent Angles: Because ΔAOB and ΔAOD are congruent, their corresponding angles are also congruent. This implies that ∠BAO = ∠DAO. This shows that diagonal AC bisects ∠A.
-
Repeating the Process: We can repeat this process for the other vertices. By considering triangles ΔBOC, ΔCOD, ΔDOA, and ΔAOB, we can similarly prove that the diagonals bisect angles B, C, and D.
Therefore, the diagonals of a rhombus bisect its vertex angles.
Implications and Connections to Other Shapes
The property of diagonals bisecting vertex angles in a rhombus has far-reaching implications and connections to other geometric shapes. Let's explore some key relationships:
-
Squares: A square is a special case of a rhombus where all angles are 90 degrees. The diagonal bisection property still holds true; the diagonals of a square bisect the right angles, resulting in 45-degree angles. This makes the diagonals perpendicular bisectors of each other.
-
Rectangles: While a rectangle has its diagonals bisect each other, they do not necessarily bisect the vertex angles unless it is also a square. This highlights the unique characteristic of the rhombus.
-
Parallelograms: All parallelograms have diagonals that bisect each other. However, only rhombuses (and squares) have diagonals that bisect the vertex angles. This emphasizes the rhombus as a special type of parallelogram with additional properties.
Applications of the Diagonal Bisection Property
The property that diagonals of a rhombus bisect its vertex angles is not merely a theoretical concept; it finds practical applications in several areas:
-
Construction and Engineering: Understanding the properties of rhombuses is essential in structural design. The predictable angles created by the bisected vertices are useful in creating stable and symmetrical structures.
-
Computer Graphics and Design: In computer-aided design (CAD) and computer graphics, the rhombus's properties are used to create various geometric shapes and patterns. The predictable angle bisection allows for precise control over the shape and orientation of elements in a design.
-
Tessellations: Rhombuses are frequently used in creating tessellations – repeating patterns that cover a plane without gaps or overlaps. The bisection property of the diagonals facilitates the creation of intricate and visually appealing designs.
-
Physics and Mechanics: The symmetrical nature of a rhombus, stemming from its diagonal properties, finds applications in various mechanical systems and force analysis. Understanding the angles created by the diagonals helps in calculations involving forces and their directions.
Advanced Concepts and Further Exploration
For those seeking a deeper understanding, here are some advanced concepts related to the diagonal bisection property of a rhombus:
-
Coordinate Geometry: Representing a rhombus on a coordinate plane allows us to use algebraic methods to verify the diagonal bisection property. This involves using distance and slope formulas to demonstrate the equality of angles.
-
Vectors: Vectors can be used to represent the sides and diagonals of a rhombus. Vector operations can then be employed to prove the bisection property in a more abstract yet powerful way.
-
Trigonometry: Trigonometric functions can be applied to analyze the relationships between the angles, side lengths, and diagonal lengths of a rhombus. This allows for more sophisticated calculations and problem-solving.
Conclusion: The Significance of a Simple Geometric Property
The seemingly simple property that the diagonals of a rhombus bisect its vertex angles is far more significant than it initially appears. This property underpins a wealth of mathematical concepts and finds practical applications in diverse fields. From structural engineering to computer graphics, understanding this property is key to unlocking deeper insights into the geometry of shapes and their practical uses. By grasping this fundamental concept, we expand our understanding of geometric relationships and their influence on our world. This exploration provides a robust foundation for further study in geometry and related fields, showcasing the elegance and power of mathematical principles in solving real-world problems. The inherent beauty of mathematical symmetry is clearly demonstrated in the rhombus and its fascinating properties.
Latest Posts
Latest Posts
-
How Many Inches In 55 Cm
Apr 05, 2025
-
5 Is What Percentage Of 8
Apr 05, 2025
-
25 24 As A Mixed Number
Apr 05, 2025
-
Calculating Mole Fraction In A Gas Mixture
Apr 05, 2025
-
Do Prokaryotes Have A Golgi Apparatus
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about Diagonals Of Rhombus Bisect Vertex Angles . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
