5 Is What Percentage Of 8
Kalali
Apr 05, 2025 · 5 min read
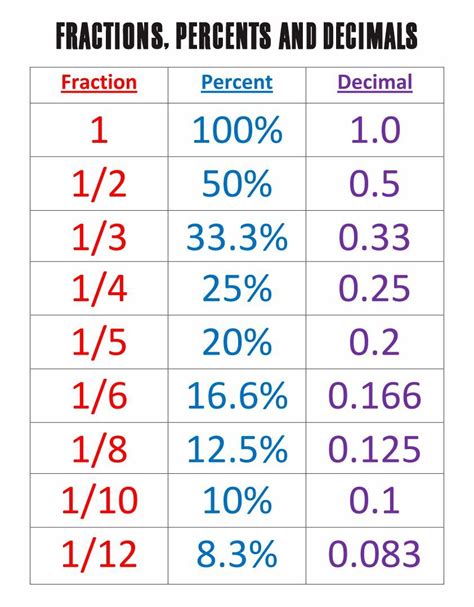
Table of Contents
5 is What Percentage of 8? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill with wide-ranging applications in daily life, from calculating discounts and taxes to analyzing data and interpreting statistics. This article delves into the question, "5 is what percentage of 8?", providing a step-by-step explanation, exploring different methods of calculation, and demonstrating how this type of problem can be solved in various contexts. We'll also touch upon the broader applications of percentage calculations and offer tips for mastering this essential mathematical concept.
Understanding Percentages: The Basics
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "per hundred." For example, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5. Percentages are a convenient way to compare proportions and make relative comparisons between different quantities.
Method 1: Using the Formula
The most straightforward method for calculating percentages involves using a simple formula:
(Part / Whole) x 100% = Percentage
In our case:
- Part: 5
- Whole: 8
Plugging these values into the formula, we get:
(5 / 8) x 100% = 0.625 x 100% = 62.5%
Therefore, 5 is 62.5% of 8.
Method 2: Proportion Method
Another approach involves setting up a proportion. We can represent the problem as:
5 / 8 = x / 100
Where 'x' represents the percentage we're trying to find. To solve for 'x', we can cross-multiply:
8x = 500
Then, divide both sides by 8:
x = 500 / 8 = 62.5
Therefore, 5 is 62.5% of 8. This method is particularly helpful in visualizing the relationship between the parts and the whole.
Method 3: Decimal Conversion
This method involves first converting the fraction 5/8 into a decimal and then multiplying by 100 to express it as a percentage.
5 divided by 8 equals 0.625. Multiplying this decimal by 100 gives us 62.5%.
Thus, 5 is 62.5% of 8. This method is efficient and relies on a basic understanding of decimal conversions.
Real-World Applications of Percentage Calculations
Understanding how to calculate percentages is essential in a wide variety of situations, including:
1. Financial Calculations:
- Discounts: Calculating the discounted price of an item after a percentage discount is applied. For example, a 20% discount on a $100 item would result in a $20 discount, leaving a final price of $80.
- Taxes: Determining the amount of sales tax or income tax payable on earnings or purchases.
- Interest Rates: Calculating simple or compound interest earned on savings accounts or paid on loans.
- Investment Returns: Assessing the percentage return on investments over a specific period.
2. Data Analysis and Interpretation:
- Statistical analysis: Representing data proportions and trends using percentages. For example, the percentage of students who passed an exam or the percentage change in a company's sales figures.
- Surveys and polls: Reporting results and interpreting the significance of survey findings.
- Scientific studies: Expressing experimental results and drawing conclusions based on percentage changes or proportions.
3. Everyday Life:
- Tipping: Calculating the appropriate tip amount in a restaurant.
- Cooking and Baking: Adjusting recipe quantities based on percentage increases or decreases.
- Shopping: Comparing prices and values based on discounts and unit prices.
Tips for Mastering Percentage Calculations
- Practice regularly: The more you practice, the more comfortable you'll become with these calculations. Try solving different percentage problems to reinforce your understanding.
- Use online calculators and tools: Several online resources offer percentage calculators that can quickly and accurately solve percentage problems. These can be helpful for checking your work and for solving more complex problems.
- Understand the underlying concepts: Focus on understanding the core concepts of percentages, fractions, and decimals, as these are fundamental to solving percentage problems effectively.
- Break down complex problems: If faced with a complex percentage problem, break it down into smaller, more manageable steps. This will help you avoid errors and make the problem easier to solve.
- Learn different methods: Familiarize yourself with various methods of solving percentage problems, such as the formula method, the proportion method, and the decimal conversion method. This will give you flexibility in choosing the most appropriate method for a given problem.
Expanding on the Problem: Variations and Extensions
The core problem "5 is what percentage of 8?" can be expanded to explore similar problems with slightly different contexts. For instance:
- Finding the whole: If 25% of a number is 5, what is the number? (This involves rearranging the percentage formula to solve for the whole.)
- Finding the part: What is 62.5% of 12? (This involves applying the percentage formula to find the part.)
- Percentage increase/decrease: If a quantity increases from 8 to 10, what is the percentage increase? (This involves finding the difference, dividing it by the original quantity, and multiplying by 100%.)
- Multiple percentages: What is 20% of 30% of 100? (This involves solving the percentages sequentially.)
Mastering these variations will solidify your understanding of percentage calculations and their practical applications.
Conclusion: The Importance of Percentage Skills
The ability to accurately and efficiently calculate percentages is a crucial skill with far-reaching implications across numerous aspects of life. From managing finances to interpreting data and making informed decisions, a strong understanding of percentages provides a valuable tool for navigating the complexities of the modern world. By practicing consistently and understanding the underlying concepts, you can master this essential mathematical skill and enhance your ability to solve a variety of problems, both simple and complex. Remember that consistent practice and understanding the different approaches will ultimately lead to mastery of percentage calculations. The core principle remains consistent: understanding the relationship between the part, the whole, and the percentage itself.
Latest Posts
Latest Posts
-
8 Is What Percent Of 2
Apr 06, 2025
-
How Many Liters Are In 8 Gallons
Apr 06, 2025
-
What Is 32 Degrees Fahrenheit In Celsius
Apr 06, 2025
-
1 3 To The Power Of 3
Apr 06, 2025
-
What Is 30 Off Of 60
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about 5 Is What Percentage Of 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
