Domain And Range Of Trig Functions
Kalali
Mar 27, 2025 · 6 min read
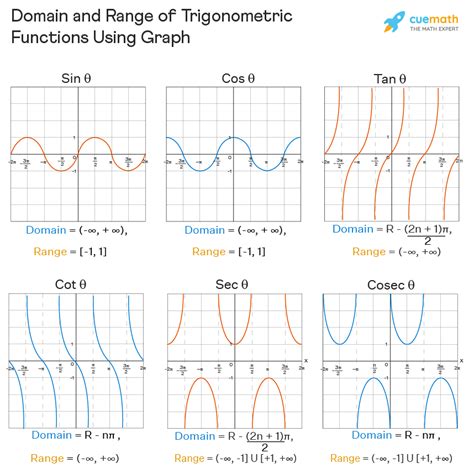
Table of Contents
- Domain And Range Of Trig Functions
- Table of Contents
- Domain and Range of Trigonometric Functions: A Comprehensive Guide
- Understanding Domain and Range
- The Six Trigonometric Functions
- 1. Sine (sin x)
- 2. Cosine (cos x)
- 3. Tangent (tan x)
- 4. Cosecant (csc x)
- 5. Secant (sec x)
- 6. Cotangent (cot x)
- Practical Applications and Considerations
- Conclusion
- Latest Posts
- Latest Posts
- Related Post
Domain and Range of Trigonometric Functions: A Comprehensive Guide
Trigonometric functions, often shortened to "trig functions," are fundamental to the study of mathematics, particularly in calculus, geometry, and physics. Understanding their domains and ranges is crucial for manipulating and applying these functions correctly. This comprehensive guide will delve into the domains and ranges of the six main trigonometric functions – sine, cosine, tangent, cosecant, secant, and cotangent – providing clear explanations, visuals, and practical examples.
Understanding Domain and Range
Before we dive into the specifics of each trigonometric function, let's define the key terms:
-
Domain: The domain of a function is the set of all possible input values (often denoted as x) for which the function is defined. In simpler terms, it's all the numbers you can plug in to the function and get a meaningful output.
-
Range: The range of a function is the set of all possible output values (often denoted as y or f(x)) that the function can produce. It's all the numbers the function can give you back.
The Six Trigonometric Functions
Let's explore the domain and range of each of the six primary trigonometric functions:
1. Sine (sin x)
The sine function, denoted as sin(x), is defined as the ratio of the opposite side to the hypotenuse in a right-angled triangle. However, it extends beyond this geometric definition to encompass all real numbers.
-
Domain: The domain of sin(x) is all real numbers, represented as (-∞, ∞). You can input any real number into the sine function.
-
Range: The range of sin(x) is [-1, 1]. The output of the sine function will always be a value between -1 and 1, inclusive. This is because the ratio of the opposite side to the hypotenuse can never be greater than 1 (since the hypotenuse is always the longest side) or less than -1.
Visual Representation: The graph of sin(x) oscillates between -1 and 1, never exceeding these limits. This visually confirms the range.
2. Cosine (cos x)
The cosine function, denoted as cos(x), is defined as the ratio of the adjacent side to the hypotenuse in a right-angled triangle. Similar to sine, its definition extends to all real numbers.
-
Domain: The domain of cos(x) is all real numbers, (-∞, ∞).
-
Range: The range of cos(x) is [-1, 1]. Just like sine, the ratio of the adjacent side to the hypotenuse is always between -1 and 1.
Visual Representation: The graph of cos(x) also oscillates between -1 and 1, confirming its range. Note the phase shift compared to the sine graph.
3. Tangent (tan x)
The tangent function, denoted as tan(x), is defined as the ratio of the opposite side to the adjacent side in a right-angled triangle. This function has a significantly different domain and range compared to sine and cosine.
-
Domain: The domain of tan(x) is all real numbers except for values where the adjacent side is zero. This occurs at odd multiples of π/2 (π/2, 3π/2, 5π/2, etc.). The domain is therefore all real numbers excluding these points. We can express this as (-∞, ∞) \ { (2n+1)π/2 | n ∈ Z }, where Z represents the set of integers.
-
Range: The range of tan(x) is all real numbers, (-∞, ∞). The ratio of opposite to adjacent can take on any value, positive or negative, including arbitrarily large values as the angle approaches the asymptotes.
Visual Representation: The graph of tan(x) has vertical asymptotes at odd multiples of π/2, reflecting the restrictions on its domain and illustrating its unbounded range.
4. Cosecant (csc x)
The cosecant function, denoted as csc(x), is the reciprocal of the sine function: csc(x) = 1/sin(x). Its domain and range are determined by this relationship.
-
Domain: Since csc(x) is undefined wherever sin(x) = 0, the domain of csc(x) is all real numbers except for integer multiples of π (0, π, 2π, -π, etc.). Expressed formally: (-∞, ∞) \ {nπ | n ∈ Z}.
-
Range: The range of csc(x) is (-∞, -1] ∪ [1, ∞). Because csc(x) is the reciprocal of sin(x), its absolute value will always be greater than or equal to 1.
Visual Representation: The graph of csc(x) displays vertical asymptotes at integer multiples of π and never intersects the interval (-1, 1).
5. Secant (sec x)
The secant function, denoted as sec(x), is the reciprocal of the cosine function: sec(x) = 1/cos(x). Its domain and range follow directly from this relationship.
-
Domain: Since sec(x) is undefined wherever cos(x) = 0, the domain of sec(x) is all real numbers except for odd multiples of π/2 ((2n+1)π/2, where n is an integer). Expressed formally: (-∞, ∞) \ { (2n+1)π/2 | n ∈ Z}.
-
Range: The range of sec(x) is (-∞, -1] ∪ [1, ∞). The absolute value of sec(x) will always be greater than or equal to 1.
Visual Representation: The graph of sec(x) displays vertical asymptotes at odd multiples of π/2 and never intersects the interval (-1, 1).
6. Cotangent (cot x)
The cotangent function, denoted as cot(x), is the reciprocal of the tangent function: cot(x) = 1/tan(x) = cos(x)/sin(x). Its domain and range are defined by this relationship.
-
Domain: cot(x) is undefined wherever sin(x) = 0, so the domain of cot(x) is all real numbers except for integer multiples of π (nπ, where n is an integer). Expressed formally: (-∞, ∞) \ {nπ | n ∈ Z}.
-
Range: The range of cot(x) is all real numbers, (-∞, ∞).
Visual Representation: The graph of cot(x) exhibits vertical asymptotes at integer multiples of π, similar to tan(x), but with a different phase shift. The graph demonstrates its unbounded range.
Practical Applications and Considerations
Understanding the domains and ranges of trigonometric functions is essential for various applications:
-
Solving Trigonometric Equations: Knowing the range helps determine if a solution is valid. For instance, if an equation implies sin(x) = 2, there is no solution because the range of sine is [-1, 1].
-
Graphing Trigonometric Functions: Understanding the domain reveals where the function is defined and where there are asymptotes. Understanding the range determines the vertical extent of the graph.
-
Calculus: When working with derivatives and integrals of trigonometric functions, the domain and range play a crucial role in determining the intervals of convergence and validity of results.
-
Physics and Engineering: Trigonometric functions are essential for modeling oscillatory and periodic phenomena, such as wave motion and AC circuits. Understanding their domains and ranges is critical for accurately modeling these systems.
Conclusion
The domains and ranges of trigonometric functions are fundamental concepts in mathematics and its applications. While memorizing them is helpful, a deeper understanding of their definitions and relationships – particularly the reciprocal relationships – allows for a more intuitive grasp of these critical aspects of trigonometric functions. By visualizing their graphs and considering their geometric interpretations, one can develop a strong foundation for working with these essential mathematical tools. This detailed exploration should equip you with the knowledge to confidently handle trigonometric functions in various mathematical and real-world scenarios. Remember to always consider the domain restrictions when working with these functions to avoid errors and ensure accuracy in your calculations and applications.
Latest Posts
Latest Posts
-
How Many Electrons Does Cl Have
Mar 31, 2025
-
100 Mm Equals How Many Inches
Mar 31, 2025
-
How Tall Is 59 In In Feet
Mar 31, 2025
-
How Many Cm Is 8 Feet
Mar 31, 2025
-
What Category Of Stars Is Hot But Not Very Luminous
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about Domain And Range Of Trig Functions . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
