Dos Pares De Angulos Alternos Internos Ejemplos
Kalali
Apr 02, 2025 · 6 min read
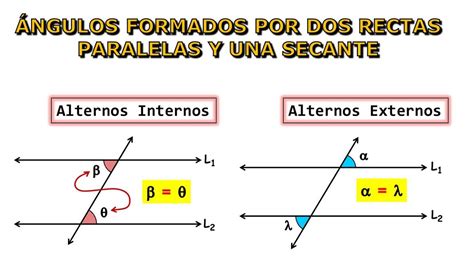
Table of Contents
Dos Pares de Ángulos Alternos Internos: Ejemplos y Explicaciones
This comprehensive guide delves into the fascinating world of alternate interior angles, exploring their properties, providing numerous examples, and demonstrating their practical applications in geometry and beyond. Understanding alternate interior angles is crucial for mastering geometry concepts and solving various mathematical problems. This article is optimized for search engines using relevant keywords and semantic variations to ensure high visibility and organic ranking.
What are Alternate Interior Angles?
Before we dive into examples, let's define what alternate interior angles are. When two parallel lines are intersected by a transversal line (a line that crosses both parallel lines), several pairs of angles are formed. Alternate interior angles are a specific pair of angles located inside the parallel lines and on opposite sides of the transversal. Crucially, they are not adjacent angles. They have a unique relationship: they are always equal in measure.
This equality is a fundamental theorem in geometry, offering a powerful tool for solving problems involving parallel lines and angles. Understanding this relationship opens the door to numerous applications in various fields.
Identifying Alternate Interior Angles:
Identifying alternate interior angles requires a careful observation of the diagram. Here's a breakdown of the key characteristics:
-
Parallel Lines: The existence of two parallel lines is a prerequisite. These lines are usually denoted by arrows on the lines indicating parallelism.
-
Transversal Line: A line intersecting the parallel lines is necessary. This line creates the angles we're interested in.
-
Interior Angles: The angles formed between the parallel lines are called interior angles.
-
Opposite Sides: Alternate interior angles are located on opposite sides of the transversal.
-
Non-adjacent: They are not next to each other; they're separated by the transversal.
Examples of Alternate Interior Angles:
Let's illustrate with some examples:
Example 1: Simple Parallel Lines
Imagine two parallel lines, l and m, intersected by a transversal line, t. Let's label the angles formed as follows:
l
/ \
/ \
/ \
/ \
t---------t
\ /
\ /
\ /
\ /
m
In this simple diagram, angles 3 and 6 are a pair of alternate interior angles, as are angles 4 and 5. If we know the measure of angle 3, we automatically know the measure of angle 6 because they are equal.
Example 2: More Complex Diagram
Let's consider a slightly more complex scenario:
l
/ \
/ \
/ \ a
/ \
t---------t
\ / b
\ /
\ / c
\ /
m
Here, angles 'a' and 'c' represent a pair of alternate interior angles. Similarly, other pairs may exist depending on the labeling. The key is to identify the parallel lines, the transversal, and the angles inside the parallel lines and on opposite sides of the transversal.
Example 3: Real-World Application (Railroad Tracks)
Think of railroad tracks. The two rails represent parallel lines. A road crossing the tracks acts as the transversal. The angles formed by the intersection of the road and the rails illustrate alternate interior angles. These angles are equal, a geometric principle employed in the design and construction of such infrastructure.
Example 4: Architectural Design
In architectural drawings, parallel lines and transversals are frequently used. Understanding alternate interior angles is vital for ensuring accuracy in designs, such as window placements, structural supports, and other elements that need to align perfectly. The angles involved are often alternate interior angles, and their equality is crucial for structural integrity and aesthetic appeal.
Example 5: Street Planning
City planners use geometric principles extensively in designing road networks. Parallel streets intersected by cross streets create numerous pairs of alternate interior angles. Understanding these angles is essential for optimizing traffic flow, ensuring safe intersections, and creating efficient urban layouts. The angles involved are often alternate interior angles, requiring precise calculations for successful planning.
Proof of the Alternate Interior Angles Theorem:
While the examples illustrate the relationship, let's delve into a brief proof of why alternate interior angles are equal when two parallel lines are cut by a transversal:
The proof often involves utilizing the concept of consecutive interior angles (supplementary angles) and vertical angles (equal angles). By demonstrating that alternate interior angles are equal to the same vertical angle or supplementary to consecutive interior angles, we can establish their equality. A complete proof requires a formal geometric approach with axioms and postulates, and is best explored in a formal geometry textbook.
Solving Problems using Alternate Interior Angles:
Let's look at some problem-solving examples:
Problem 1:
Two parallel lines are intersected by a transversal. One alternate interior angle measures 70 degrees. What is the measure of the other alternate interior angle?
Solution: Since alternate interior angles are equal, the other alternate interior angle also measures 70 degrees.
Problem 2:
In a diagram, two parallel lines are intersected by a transversal. Two alternate interior angles are represented by the expressions 2x + 10 and 3x - 5. Find the value of x and the measure of the angles.
Solution: Set the expressions equal to each other (2x + 10 = 3x - 5). Solve for x (x = 15). Substitute x back into either expression to find the angle measure (2(15) + 10 = 40 degrees). Both alternate interior angles measure 40 degrees.
Problem 3: A More Complex Scenario
Consider a more challenging problem involving multiple transversals and parallel lines. Use the properties of alternate interior angles, along with other angle relationships (vertical angles, supplementary angles), to solve for unknown angles step-by-step. Carefully label each angle and systematically work through the relationships. This often involves a chain of deductions using multiple angle properties.
Applications Beyond Geometry:
The concept of alternate interior angles extends beyond the realm of pure geometry. It finds practical applications in:
-
Computer Graphics: In computer-aided design (CAD) and 3D modeling, understanding angles is crucial for creating accurate and realistic representations.
-
Surveying and Mapping: Surveyors use geometric principles to measure distances and angles to create accurate maps and land surveys. Alternate interior angles play a significant role in determining precise measurements.
-
Engineering: Engineers use geometric concepts extensively in structural design, ensuring stability and efficiency in buildings, bridges, and other structures. The alignment and angles in these structures often rely on the properties of alternate interior angles.
Conclusion:
Understanding alternate interior angles is fundamental to mastering geometry and solving a wide range of mathematical problems. This article has provided a comprehensive overview of the concept, illustrated with various examples, and explored its practical applications in different fields. The key takeaway is that alternate interior angles provide a powerful tool for solving problems involving parallel lines and transversal lines, finding applications in various real-world scenarios, from architectural design to urban planning. By mastering this concept, you will enhance your geometrical understanding and problem-solving skills significantly. Remember to practice regularly and explore different problem types to solidify your understanding.
Latest Posts
Latest Posts
-
Do Covalent Bonds Give Water A Low Heat Capacity
Apr 03, 2025
-
187 Out Of 200 As A Percentage
Apr 03, 2025
-
At What Temp Does Water Evaporate
Apr 03, 2025
-
What Is 94 Cm In Inches
Apr 03, 2025
-
How Many Ounces In 75 Cup
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Dos Pares De Angulos Alternos Internos Ejemplos . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
