How Do You Calculate Average Kinetic Energy
Kalali
Mar 29, 2025 · 5 min read
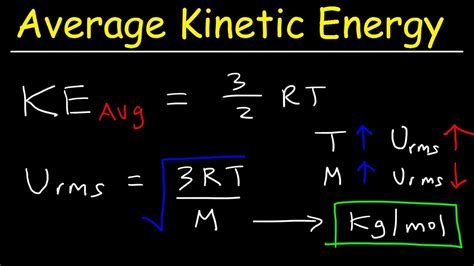
Table of Contents
How Do You Calculate Average Kinetic Energy? A Comprehensive Guide
Understanding average kinetic energy is crucial in various fields, from physics and chemistry to engineering and environmental science. This comprehensive guide will delve into the intricacies of calculating average kinetic energy, exploring different scenarios and providing clear, step-by-step explanations. We'll cover the fundamental concepts, formulas, and practical applications, equipping you with a thorough understanding of this important concept.
What is Kinetic Energy?
Before we dive into calculating average kinetic energy, let's establish a firm grasp of kinetic energy itself. Kinetic energy is the energy an object possesses due to its motion. A stationary object has zero kinetic energy. The faster an object moves, the greater its kinetic energy. This energy can be transferred to other objects through collisions or interactions.
The fundamental formula for kinetic energy (KE) is:
KE = ½ * m * v²
Where:
- KE represents kinetic energy (typically measured in Joules (J))
- m represents the mass of the object (typically measured in kilograms (kg))
- v represents the velocity of the object (typically measured in meters per second (m/s))
Why Average Kinetic Energy?
Often, we don't deal with objects moving at a constant velocity. Consider a gas molecule in a container – it's constantly colliding with other molecules and the container walls, resulting in a constantly changing velocity. In such scenarios, calculating the average kinetic energy provides a more meaningful and representative measure of the system's energy.
The average kinetic energy provides insights into the overall energy distribution within a system, particularly useful when dealing with:
- Ideal Gases: Understanding the average kinetic energy of gas molecules is essential for explaining gas laws like Boyle's Law and Charles' Law.
- Statistical Mechanics: This branch of physics uses statistical methods to analyze the behavior of large systems, and average kinetic energy is a central parameter.
- Thermodynamics: Average kinetic energy is directly related to temperature, making it a critical factor in understanding heat transfer and thermodynamic processes.
- Chemical Reactions: The average kinetic energy of reactant molecules influences the reaction rate. Higher average kinetic energy leads to more frequent and energetic collisions, increasing the likelihood of a reaction.
Calculating Average Kinetic Energy: Different Approaches
The method for calculating average kinetic energy depends on the context and the nature of the system. Let's explore several key approaches:
1. Average Kinetic Energy of a Single Object with Varying Velocity
If an object's velocity changes over time, we can determine its average kinetic energy by calculating the average of its kinetic energy at different points in time. This involves measuring the velocity at multiple instances and calculating the corresponding kinetic energy for each instance. Then, the average of these kinetic energy values is determined.
Example: An object has velocities of 2 m/s, 4 m/s, and 6 m/s at different times. Assume its mass is 1 kg.
- KE₁ = ½ * 1 kg * (2 m/s)² = 2 J
- KE₂ = ½ * 1 kg * (4 m/s)² = 8 J
- KE₃ = ½ * 1 kg * (6 m/s)² = 18 J
Average KE = (2 J + 8 J + 18 J) / 3 = 9.33 J (approximately)
2. Average Kinetic Energy of an Ideal Gas
For an ideal gas, the average kinetic energy is directly proportional to its absolute temperature. This relationship is expressed by the following equation:
KE<sub>avg</sub> = (3/2) * k<sub>B</sub> * T
Where:
- KE<sub>avg</sub> represents the average kinetic energy of a gas molecule.
- k<sub>B</sub> is the Boltzmann constant (approximately 1.38 x 10⁻²³ J/K)
- T is the absolute temperature of the gas (measured in Kelvin (K))
This formula is remarkably powerful because it links a microscopic property (kinetic energy of individual molecules) to a macroscopic property (temperature). It's crucial to note that this equation applies only to ideal gases, which are theoretical gases that obey certain assumptions (e.g., negligible intermolecular forces and negligible molecular volume).
3. Average Kinetic Energy Using Statistical Mechanics
For more complex systems, statistical mechanics provides a more rigorous approach. This involves using probability distributions (such as the Maxwell-Boltzmann distribution for gases) to describe the distribution of molecular velocities. The average kinetic energy is then calculated by integrating over this distribution. This is a more advanced technique, requiring a strong understanding of calculus and statistical methods.
The calculations involved here are often quite complex and typically require specialized software or computational tools. The underlying principle, however, remains the same: determining the average kinetic energy from the distribution of energies of individual particles within the system.
4. Average Kinetic Energy from Experimental Data
In experimental settings, measuring the average kinetic energy might involve indirect methods. For instance, you could measure the temperature of a gas and use the ideal gas law equation mentioned above. Alternatively, you might study the momentum transfer during collisions and infer the average kinetic energy from the observed changes in momentum. Analyzing experimental data often requires statistical analysis to handle uncertainties and experimental error.
Practical Applications of Average Kinetic Energy
The concept of average kinetic energy finds wide applications across various scientific and engineering disciplines:
- Understanding Gas Behavior: The average kinetic energy explains gas pressure, diffusion, and effusion. Higher average kinetic energy translates to higher pressure and faster diffusion rates.
- Chemical Kinetics: Reaction rates depend on the average kinetic energy of reactant molecules. Higher average kinetic energy leads to more frequent and energetic collisions, hence accelerating the reaction.
- Thermodynamics and Heat Transfer: Heat transfer is fundamentally the transfer of kinetic energy. Understanding average kinetic energy is crucial for analyzing heat flow, thermal equilibrium, and related concepts.
- Fluid Mechanics: The average kinetic energy of fluid particles plays a vital role in understanding fluid flow, pressure gradients, and turbulence.
- Material Science: The average kinetic energy of atoms in a solid influences its material properties, such as thermal conductivity and strength.
- Astrophysics: Understanding the average kinetic energy of stars and gas clouds is crucial for modeling stellar evolution and galactic dynamics.
Conclusion
Calculating average kinetic energy is a fundamental concept with widespread applications. The specific method depends on the system's nature and available information. While simple cases involve direct calculations using the basic kinetic energy formula and averaging velocities, more complex scenarios necessitate advanced statistical methods. Understanding the concepts behind these calculations provides a powerful tool for analyzing and predicting the behavior of various systems, from simple objects to complex gases and beyond. The ability to accurately calculate and interpret average kinetic energy is a valuable asset for anyone working in science, engineering, or related fields. Remember that precision and understanding of the underlying assumptions are crucial for accurate results.
Latest Posts
Latest Posts
-
How Long Is 2 Hours In Minutes
Mar 31, 2025
-
What Is 20 Of 70 Dollars
Mar 31, 2025
-
What Is 3 20 As A Percentage
Mar 31, 2025
-
1000 Km Is How Many Miles
Mar 31, 2025
-
What Is The Average Atomic Mass Of Silver
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about How Do You Calculate Average Kinetic Energy . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
