How Many Acute Angles Does An Acute Triangle Have
Kalali
Apr 03, 2025 · 6 min read
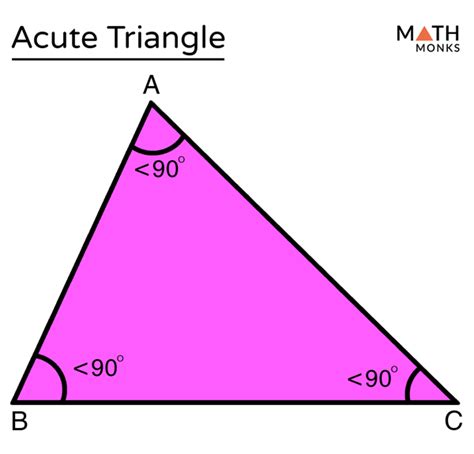
Table of Contents
How Many Acute Angles Does an Acute Triangle Have? A Deep Dive into Geometry
Understanding the properties of triangles is fundamental to geometry. This article delves into the specifics of acute triangles, exploring the definition, characteristics, and answering the core question: how many acute angles does an acute triangle possess? We will also touch upon related concepts, clarifying common misconceptions and offering a comprehensive understanding of this geometrical shape.
Defining Acute Triangles
Before we dive into the number of acute angles, let's establish a clear definition. A triangle, as you likely know, is a polygon with three sides and three angles. There are several classifications of triangles based on their angles:
- Acute Triangle: A triangle where all three angles are acute angles (less than 90 degrees).
- Right Triangle: A triangle containing one right angle (exactly 90 degrees).
- Obtuse Triangle: A triangle with one obtuse angle (greater than 90 degrees).
The focus of our discussion is the acute triangle. It's characterized by its three angles, each measuring less than 90 degrees. This seemingly simple definition holds significant implications for the triangle's properties and characteristics.
The Fundamental Theorem: Three Acute Angles
The answer to our main question is straightforward: An acute triangle has three acute angles. This is the very definition of an acute triangle. There's no exception to this rule. If a triangle has fewer than three acute angles, or if it has any angle greater than or equal to 90 degrees, it's not an acute triangle. It's crucial to understand that this is not a theorem to be proven; it's the very foundation of the definition of an acute triangle.
Exploring the Properties of Acute Triangles
While the number of acute angles defines an acute triangle, several other properties are worth exploring:
Angle Sum Theorem
The Angle Sum Theorem states that the sum of the angles in any triangle is always 180 degrees. This theorem holds true regardless of whether the triangle is acute, right, or obtuse. For an acute triangle, since all three angles are less than 90 degrees, their sum must still equal 180 degrees. This is a critical point to remember; it reinforces the fact that while each angle is individually less than 90 degrees, their collective sum always results in 180 degrees.
Side Length Relationships
Unlike right triangles where the Pythagorean theorem defines a relationship between side lengths, acute triangles don't have a single, universally applicable equation to relate their side lengths. However, we can make some general observations:
- No single side can be longer than the sum of the other two sides. This is a fundamental rule for all triangles, stemming from the triangle inequality theorem.
- The lengths of the sides dictate the angles. A triangle with three equal sides (an equilateral triangle) will also have three equal angles (60 degrees each), which is a specific type of acute triangle. Conversely, triangles with unequal side lengths will have unequal angles.
Understanding these relationships allows for a more comprehensive understanding of how side lengths contribute to the overall shape and properties of the acute triangle.
Differentiating Acute Triangles from Other Triangle Types
It's essential to be able to distinguish acute triangles from right and obtuse triangles. Here's a quick comparison:
| Triangle Type | Angle Characteristics | Example Angles (degrees) |
|---|---|---|
| Acute Triangle | All three angles are less than 90 degrees | 60, 60, 60 (Equilateral) |
| 50, 60, 70 | ||
| Right Triangle | One angle is exactly 90 degrees | 90, 45, 45 |
| 90, 30, 60 | ||
| Obtuse Triangle | One angle is greater than 90 degrees | 100, 40, 40 |
| 120, 30, 30 |
This table provides a clear visual representation of the differences in angle measurements for each type of triangle. Note that the sum of angles in each case still equals 180 degrees.
Acute Triangles in Real-World Applications
Acute triangles, despite their seemingly simple definition, appear frequently in various real-world scenarios:
- Structural Engineering: Many architectural designs incorporate acute triangles for their inherent strength and stability. Think of the triangular bracing often used in bridges and buildings.
- Navigation: Triangulation, a method used in navigation and surveying, relies on the principles of acute triangles to determine precise locations.
- Computer Graphics: Acute triangles are fundamental building blocks in computer graphics and 3D modeling, enabling the creation of complex shapes and surfaces.
- Nature: You'll find acute triangles in natural formations like the shapes of certain crystals or the angles formed by branches of trees.
Understanding acute triangles and their properties is not just an academic exercise; it’s relevant to many practical applications.
Common Misconceptions and Clarifications
Some common misconceptions surround acute triangles, which we will clarify here:
- Misconception 1: All equilateral triangles are acute, but not all acute triangles are equilateral. While an equilateral triangle (with three equal sides and three 60-degree angles) is a type of acute triangle, many other acute triangles exist with unequal side lengths and angles.
- Misconception 2: Acute triangles are always similar. This is incorrect. Similarity requires corresponding angles to be equal and sides to be proportional; acute triangles can have different angle measurements and, therefore, not be similar.
- Misconception 3: The area of an acute triangle is always less than the area of a right triangle with the same side lengths. This is false. The area of a triangle depends on the base and height, and not solely on the triangle's classification.
Addressing these misconceptions is vital for a complete understanding of the properties and characteristics of acute triangles.
Advanced Concepts and Further Exploration
For those interested in delving deeper, here are some advanced concepts related to acute triangles:
- Trigonometry: Trigonometric functions (sine, cosine, tangent) are extensively used to solve problems involving the angles and side lengths of acute triangles.
- Geometric Constructions: Using a compass and straightedge, various acute triangles can be constructed, offering a practical application of geometric principles.
- Coordinate Geometry: Acute triangles can be analyzed and their properties determined using coordinate systems, providing an algebraic perspective on geometry.
Exploring these advanced concepts can provide a richer and more nuanced understanding of acute triangles and their applications in various mathematical fields.
Conclusion: The Defining Characteristic of an Acute Triangle
To reiterate, an acute triangle is defined by having three acute angles, all of which measure less than 90 degrees. This fundamental characteristic, along with the angle sum theorem and other properties, enables us to understand, analyze, and utilize acute triangles in various practical and theoretical contexts. From simple geometric exercises to complex engineering applications, the understanding of acute triangles remains a cornerstone of geometric knowledge. We have explored its properties, differentiated it from other triangle types, clarified common misconceptions, and even touched upon some advanced concepts. Hopefully, this comprehensive exploration has solidified your understanding of this important geometric shape.
Latest Posts
Latest Posts
-
An Injured Limb Should Be Kept Above Heart Level
Apr 04, 2025
-
How Many Ounces Is 1 Cup Of Butter
Apr 04, 2025
-
Does My Brain Know I Have Eyes
Apr 04, 2025
-
Common Multiples Of 4 And 14
Apr 04, 2025
-
Does Weathering Affect Different Materials Differently
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about How Many Acute Angles Does An Acute Triangle Have . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
