How Many Obtuse Angles Are In A Obtuse Triangle
Kalali
Mar 30, 2025 · 5 min read
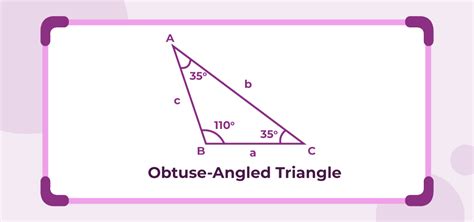
Table of Contents
How Many Obtuse Angles Are in an Obtuse Triangle?
The question, "How many obtuse angles are in an obtuse triangle?" might seem deceptively simple. The answer, however, provides a deeper understanding of fundamental geometric principles. Let's explore this seemingly straightforward question in detail, delving into the definitions, properties, and implications of obtuse triangles.
Understanding Angles and Triangles
Before tackling the core question, let's establish a firm grasp of the necessary terminology.
Angles: Acute, Right, and Obtuse
An angle is formed by two rays sharing a common endpoint (the vertex). Angles are classified based on their measure:
- Acute angle: Measures less than 90 degrees (0° < x < 90°).
- Right angle: Measures exactly 90 degrees (x = 90°).
- Obtuse angle: Measures more than 90 degrees but less than 180 degrees (90° < x < 180°).
- Straight angle: Measures exactly 180 degrees (x = 180°). This forms a straight line.
Triangles: Classifying by Angles
Triangles are classified based on the measures of their interior angles:
- Acute triangle: All three angles are acute (less than 90°).
- Right triangle: One angle is a right angle (exactly 90°).
- Obtuse triangle: One angle is an obtuse angle (greater than 90°).
The Defining Characteristic of an Obtuse Triangle
The key to answering our central question lies in the definition itself. An obtuse triangle is specifically defined as a triangle possessing one and only one obtuse angle. This is crucial. The presence of a single obtuse angle automatically excludes the possibility of having more.
Let's explore why this is the case:
The Angle Sum Theorem
The Angle Sum Theorem states that the sum of the interior angles of any triangle is always 180 degrees. This theorem is fundamental to Euclidean geometry and is the cornerstone for understanding why an obtuse triangle can only have one obtuse angle.
Suppose, for the sake of contradiction, that a triangle had two obtuse angles. Let's say these obtuse angles measure 'x' and 'y' degrees, where both x and y are greater than 90 degrees. The sum of these two angles alone (x + y) would already be greater than 180 degrees (90° + 90° = 180°). However, the third angle, 'z', would also need to be added to this sum, making the total sum (x + y + z) greater than 180 degrees. This contradicts the Angle Sum Theorem. Therefore, a triangle cannot have more than one obtuse angle.
Visualizing the Impossibility
Imagine trying to construct a triangle with two obtuse angles. As you attempt to draw the angles, you'll quickly discover that the lines forming the sides will never meet to close the triangle. The sum of the angles will exceed 180 degrees, preventing the formation of a closed, triangular shape. This visual demonstration reinforces the mathematical proof derived from the Angle Sum Theorem.
The Uniqueness of Obtuse Triangles
The restriction to only one obtuse angle fundamentally shapes the properties and characteristics of obtuse triangles, distinguishing them from acute and right triangles. This single obtuse angle dictates several other characteristics, such as:
-
Side Lengths: The side opposite the obtuse angle is always the longest side of the triangle. This follows from the fact that larger angles subtend larger sides.
-
Altitude: The altitude drawn from the vertex of the obtuse angle always falls outside the triangle. This is because the obtuse angle is greater than 90 degrees, preventing the altitude from falling within the triangle's boundaries.
-
Area Calculation: While the standard formula (1/2 * base * height) still applies, determining the height in an obtuse triangle might require more careful consideration due to the external altitude.
-
Circumcircle and Incircle: Like all triangles, an obtuse triangle possesses both a circumcircle (a circle passing through all three vertices) and an incircle (a circle tangent to all three sides). However, the positions and radii of these circles are influenced by the presence of the obtuse angle.
Further Exploration: Practical Applications and Related Concepts
The concept of obtuse triangles isn't just an abstract geometric idea; it finds applications in various fields:
-
Engineering and Architecture: Understanding angles is crucial in structural design. The stability and strength of structures depend heavily on the angles used in the construction. Obtuse triangles, while less common in foundational structures than right triangles, can appear in specific architectural elements and designs.
-
Computer Graphics and Game Development: Representing and manipulating shapes in computer graphics and game development requires a thorough understanding of geometric principles, including the properties of different types of triangles.
-
Navigation and Surveying: Calculating distances and positions often relies on triangulation. The properties of obtuse triangles, like the length of their sides and the position of their altitudes, play a role in these calculations.
-
Trigonometry: The study of triangles and their angles, specifically trigonometric functions (sine, cosine, and tangent), is intimately tied to the properties of all triangles, including obtuse ones.
Conclusion: One and Only One
To reiterate the central point: an obtuse triangle, by its definition, contains exactly one obtuse angle. This is a direct consequence of the Angle Sum Theorem, which dictates that the sum of a triangle's angles must always equal 180 degrees. The presence of a single obtuse angle, greater than 90 degrees, prevents the possibility of a second obtuse angle within the same triangle. This seemingly simple answer reveals a deeper understanding of fundamental geometric concepts and their implications in various applications. Understanding this characteristic is fundamental to working with geometric shapes and solving problems related to angles and triangles.
Latest Posts
Latest Posts
-
How Many Centimeters Are In 1 Foot
Apr 01, 2025
-
Trna Uses What To Match To The Mrna
Apr 01, 2025
-
Cuanto Es 200 Centimetros En Pulgadas
Apr 01, 2025
-
How Many Ft Is 62 Inches
Apr 01, 2025
-
25 Is 30 Percent Of What Number
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about How Many Obtuse Angles Are In A Obtuse Triangle . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
