How To Calculate Average Kinetic Energy
Kalali
Mar 24, 2025 · 5 min read
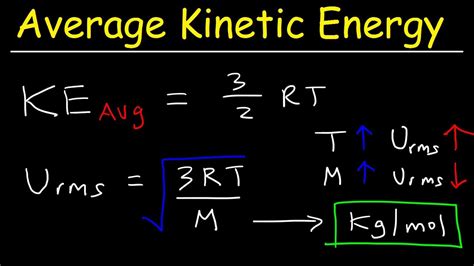
Table of Contents
How to Calculate Average Kinetic Energy: A Comprehensive Guide
Understanding average kinetic energy is crucial in various fields, from thermodynamics and statistical mechanics to understanding the behavior of gases and the properties of materials. This comprehensive guide delves into the intricacies of calculating average kinetic energy, catering to both beginners and those seeking a deeper understanding. We will explore different approaches, scenarios, and provide practical examples to solidify your comprehension.
What is Kinetic Energy?
Before diving into the calculation of average kinetic energy, let's establish a clear understanding of kinetic energy itself. Kinetic energy is the energy an object possesses due to its motion. A stationary object has zero kinetic energy. The faster an object moves, and the more massive it is, the greater its kinetic energy. The formula for kinetic energy (KE) is:
KE = 1/2 * mv²
Where:
- m represents the mass of the object (typically in kilograms).
- v represents the velocity of the object (typically in meters per second).
This formula gives us the kinetic energy of a single object moving at a specific velocity. However, many systems involve numerous particles moving at various speeds. This is where the concept of average kinetic energy becomes vital.
Calculating Average Kinetic Energy: Different Scenarios
The method for calculating average kinetic energy depends heavily on the system in question. Let's explore a few key scenarios:
1. Average Kinetic Energy of a Single Particle Over Time
Imagine tracking the motion of a single particle. Its velocity might fluctuate over time. To calculate the average kinetic energy, you wouldn't use a single velocity; instead, you'd need to consider the velocity at various points in time.
- Record Velocities: Measure or calculate the velocity (v) of the particle at multiple time intervals (t1, t2, t3... tn).
- Calculate Kinetic Energies: Use the kinetic energy formula (KE = 1/2 * mv²) to calculate the kinetic energy at each time interval. This will yield a series of KE values (KE1, KE2, KE3... KEn).
- Calculate the Average: Sum all the individual kinetic energies and divide by the number of measurements (n).
Average KE = (KE1 + KE2 + KE3 + ... + KEn) / n
This method provides the average kinetic energy of a single particle over a period, accounting for its varying velocities.
2. Average Kinetic Energy of Multiple Particles at a Single Point in Time
This scenario is common in statistical mechanics, particularly when dealing with gases. Consider a container filled with numerous gas molecules moving randomly. Each molecule possesses a different velocity and therefore a different kinetic energy.
This calculation is more complex and typically uses statistical methods. The average kinetic energy is directly proportional to the absolute temperature (T) of the system. The relationship is given by the following equation:
Average KE = (3/2) * k * T
Where:
- k is the Boltzmann constant (approximately 1.38 x 10⁻²³ J/K).
- T is the absolute temperature of the system (in Kelvin).
This equation applies to an ideal gas. Real gases deviate slightly from this ideal behavior, especially at high pressures or low temperatures.
3. Average Kinetic Energy in a System with a Distribution of Velocities (Maxwell-Boltzmann Distribution)
Real-world systems rarely contain particles all moving at the same speed. The distribution of particle velocities is often described by the Maxwell-Boltzmann distribution. This distribution shows the probability of a particle having a particular velocity at a given temperature.
Calculating the average kinetic energy using the Maxwell-Boltzmann distribution involves integration. The average kinetic energy, in this case, is still given by:
Average KE = (3/2) * k * T
This equation holds true despite the wide range of velocities in the system because the Maxwell-Boltzmann distribution itself is derived from considering the statistical mechanics of a large number of particles. The integration accounts for the probability of each velocity, resulting in the same simple average kinetic energy relationship to temperature.
Practical Examples
Let's illustrate these calculations with some examples:
Example 1: Single Particle Over Time
A 0.1 kg ball is thrown vertically upwards. Its velocities at different times are recorded as follows:
- t1 = 1s, v1 = 5 m/s
- t2 = 2s, v2 = 2 m/s
- t3 = 3s, v3 = -1 m/s (negative indicates downward motion)
-
Calculate individual KE:
- KE1 = 1/2 * (0.1 kg) * (5 m/s)² = 1.25 J
- KE2 = 1/2 * (0.1 kg) * (2 m/s)² = 0.2 J
- KE3 = 1/2 * (0.1 kg) * (-1 m/s)² = 0.05 J
-
Calculate Average KE:
- Average KE = (1.25 J + 0.2 J + 0.05 J) / 3 = 0.5 J
Example 2: Multiple Particles at a Given Temperature
Consider a sample of helium gas at 300 K. The average kinetic energy of the helium atoms can be calculated directly using the Boltzmann constant:
- Average KE = (3/2) * (1.38 x 10⁻²³ J/K) * (300 K) ≈ 6.21 x 10⁻²¹ J
This represents the average kinetic energy of a single helium atom at 300K. To find the total average kinetic energy of the entire sample, you'd need to multiply by the total number of atoms present.
Advanced Considerations
-
Non-ideal Gases: For real gases, deviations from the ideal gas law necessitate more complex calculations, often involving the use of virial coefficients or other correction factors.
-
Molecular Degrees of Freedom: The (3/2) factor in the average kinetic energy equation assumes a monatomic gas. For diatomic or polyatomic gases, additional degrees of freedom (rotation and vibration) contribute to the total energy, modifying the equation accordingly.
-
Quantum Effects: At very low temperatures, quantum effects become significant and classical mechanics may no longer accurately describe the behavior of particles.
Conclusion
Calculating average kinetic energy requires understanding the context of the system. For a single particle over time, simple averaging of individual kinetic energies is sufficient. For many-particle systems, the relationship between average kinetic energy and temperature, guided by the Boltzmann constant, provides a powerful tool for analysis. Mastering these concepts provides a strong foundation for comprehending various physical phenomena and modeling the behavior of matter. Further exploration into statistical mechanics and thermodynamics will offer a deeper understanding of the more nuanced aspects of kinetic energy calculations. Remember to always consider the specific system you're studying and the assumptions that underlie your chosen method of calculation.
Latest Posts
Latest Posts
-
How To Tell If A Triangle Is Acute
Mar 28, 2025
-
What Is 60 Degrees In Celsius
Mar 28, 2025
-
How Many Cups In 4 5 Oz
Mar 28, 2025
-
Distance Between Earth And Sun In Light Years
Mar 28, 2025
-
230 Cm Is How Many Inches
Mar 28, 2025
Related Post
Thank you for visiting our website which covers about How To Calculate Average Kinetic Energy . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
