How To Tell If A Triangle Is Acute Or Obtuse
Kalali
Mar 26, 2025 · 6 min read
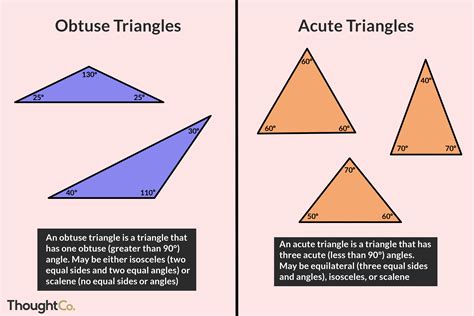
Table of Contents
How to Tell if a Triangle is Acute or Obtuse: A Comprehensive Guide
Determining whether a triangle is acute, obtuse, or right is a fundamental concept in geometry. Understanding these classifications is crucial for solving various geometric problems and builds a strong foundation for more advanced mathematical concepts. This comprehensive guide will equip you with the knowledge and techniques to confidently identify acute and obtuse triangles, covering various approaches and providing ample examples.
Understanding Triangle Classifications
Before delving into the specifics of identifying acute and obtuse triangles, let's clarify the different classifications based on their angles:
- Acute Triangle: A triangle where all three angles are less than 90 degrees.
- Obtuse Triangle: A triangle where one angle is greater than 90 degrees.
- Right Triangle: A triangle where one angle is exactly 90 degrees.
It's important to remember that the sum of the angles in any triangle always equals 180 degrees. This fundamental property is key to determining the type of triangle we're dealing with.
Method 1: Using Angle Measurement
The most straightforward method to identify an acute or obtuse triangle is by directly measuring its angles using a protractor or other angle measuring tools.
Steps:
- Measure each angle: Carefully measure each of the three angles in the triangle using a protractor. Ensure accuracy in your measurements.
- Analyze the measurements:
- Acute Triangle: If all three angles measure less than 90 degrees, the triangle is acute.
- Obtuse Triangle: If one angle measures more than 90 degrees, the triangle is obtuse.
- Right Triangle: If one angle measures exactly 90 degrees, the triangle is a right triangle.
Example:
Let's say we measure the angles of a triangle as follows: Angle A = 75 degrees, Angle B = 60 degrees, and Angle C = 45 degrees. Since all angles are less than 90 degrees, this is an acute triangle. If, instead, Angle A was 110 degrees, Angle B was 40 degrees, and Angle C was 30 degrees, it would be an obtuse triangle because Angle A is greater than 90 degrees.
Method 2: Using the Pythagorean Theorem and its Converse
The Pythagorean Theorem, a cornerstone of geometry, states that in a right-angled triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides (legs). Its converse states that if the square of the longest side of a triangle is equal to the sum of the squares of the other two sides, then the triangle is a right-angled triangle.
We can utilize the converse of the Pythagorean Theorem and a comparison of side lengths to indirectly determine if a triangle is acute or obtuse, even without directly measuring angles.
Steps:
- Identify the longest side: Determine the longest side of the triangle. Let's denote this side as 'c', and the other two sides as 'a' and 'b'.
- Apply the comparison:
- If c² < a² + b²: The triangle is acute. The square of the longest side is less than the sum of the squares of the other two sides.
- If c² > a² + b²: The triangle is obtuse. The square of the longest side is greater than the sum of the squares of the other two sides.
- If c² = a² + b²: The triangle is right. This is the Pythagorean Theorem itself.
Example:
Consider a triangle with sides a = 3, b = 4, and c = 5 (the longest side). Let's check:
c² = 5² = 25 a² + b² = 3² + 4² = 9 + 16 = 25
Since c² = a² + b², this triangle is a right triangle.
Now, consider a triangle with sides a = 2, b = 3, and c = 4.
c² = 4² = 16 a² + b² = 2² + 3² = 4 + 9 = 13
Since c² > a² + b², this triangle is obtuse.
Finally, consider a triangle with sides a = 5, b = 6, and c = 7.
c² = 7² = 49 a² + b² = 5² + 6² = 25 + 36 = 61
Since c² < a² + b², this triangle is acute.
Method 3: Using Trigonometry (Law of Cosines)
Trigonometry provides another powerful tool for determining the type of triangle. The Law of Cosines relates the lengths of the sides of a triangle to the cosine of one of its angles.
The Law of Cosines states: c² = a² + b² - 2ab cos(C)
where 'c' is the length of the side opposite angle C, and 'a' and 'b' are the lengths of the other two sides.
Steps:
- Choose an angle: Select one of the angles in the triangle (let's use angle C).
- Apply the Law of Cosines: Substitute the known side lengths into the formula.
- Solve for cos(C): Rearrange the formula to solve for cos(C).
- Analyze the result:
- If cos(C) > 0: Angle C is acute (less than 90 degrees).
- If cos(C) < 0: Angle C is obtuse (greater than 90 degrees).
- If cos(C) = 0: Angle C is a right angle (exactly 90 degrees).
- Repeat if necessary: Repeat steps 1-4 for other angles if needed to confirm the triangle's classification.
Example:
Let's consider a triangle with sides a = 6, b = 8, and c = 10. Let's find the cosine of angle C:
10² = 6² + 8² - 2(6)(8)cos(C) 100 = 36 + 64 - 96cos(C) 0 = -96cos(C) cos(C) = 0
Since cos(C) = 0, angle C is a right angle, making this a right triangle.
Combining Methods for Robust Identification
While each method provides a viable approach, combining methods often leads to a more robust and accurate identification. For instance, you could use the side length comparison method (Method 2) as a quick initial assessment, and then use angle measurement (Method 1) or the Law of Cosines (Method 3) to verify your findings. This cross-validation enhances the reliability of your triangle classification.
Practical Applications
Understanding how to classify triangles is not just a theoretical exercise; it has significant practical applications in various fields:
- Engineering and Architecture: Determining the stability and structural integrity of designs often requires analyzing the angles and side lengths of triangles within the structure.
- Surveying and Cartography: Precisely measuring angles and distances is crucial for creating accurate maps and land surveys. Triangle classifications are fundamental to these calculations.
- Computer Graphics and Game Development: Rendering realistic 3D graphics and simulating physics within games relies heavily on geometric calculations, including triangle classifications.
- Physics and Astronomy: Understanding the geometry of triangles helps in solving problems related to vectors, forces, and celestial navigation.
Conclusion
Identifying whether a triangle is acute or obtuse is a fundamental skill in geometry with far-reaching applications. By mastering the methods outlined in this guide – angle measurement, side length comparison using the Pythagorean Theorem's converse, and the application of the Law of Cosines – you can confidently classify triangles and build a strong foundation for more advanced geometric concepts. Remember that combining these techniques provides a robust and accurate approach to triangle classification, ensuring the reliability of your results across various applications.
Latest Posts
Latest Posts
-
How Many Feet Is 82 In
Mar 29, 2025
-
Half Cup Is How Many Ml
Mar 29, 2025
-
How Many Sides Does Rhombus Have
Mar 29, 2025
-
Number Of Valence Electrons For Potassium
Mar 29, 2025
-
How Much Is 7 8 In Inches
Mar 29, 2025
Related Post
Thank you for visiting our website which covers about How To Tell If A Triangle Is Acute Or Obtuse . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
