Integral Of 1 1 X 2 3 2
Kalali
Jun 08, 2025 · 2 min read
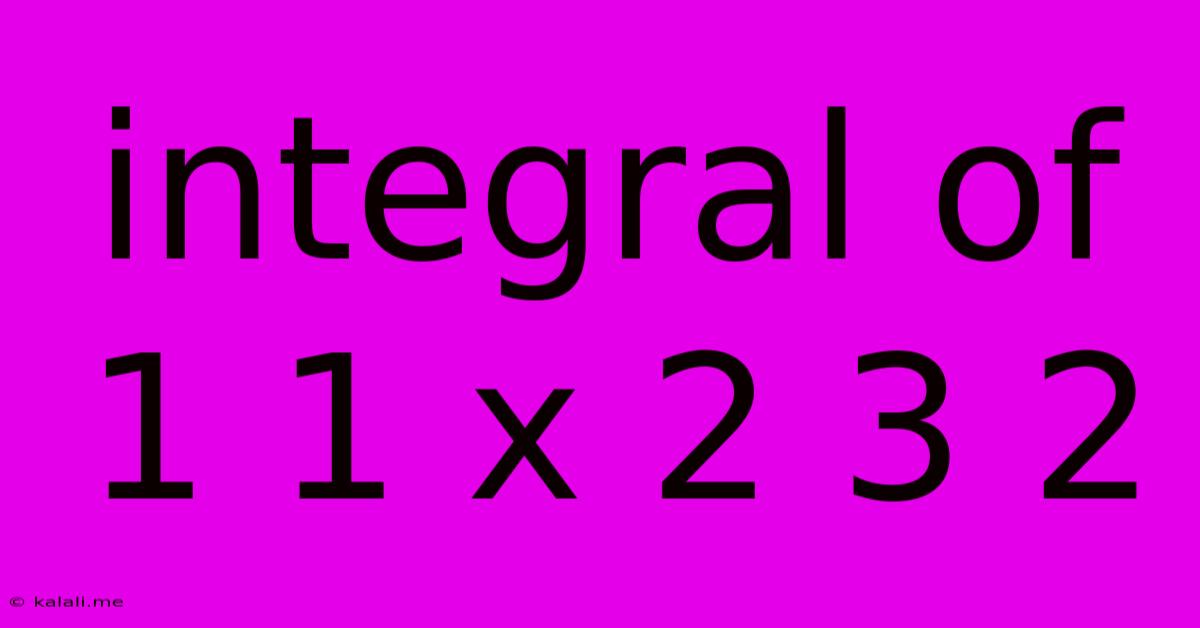
Table of Contents
Solving the Integral of 1/(1 + x^2)^(3/2)
This article will guide you through the process of solving the definite integral of 1/(1 + x²)^(3/2). This integral is a common challenge in calculus, often appearing in problems involving arc length calculations and trigonometric substitutions. Understanding how to solve this type of integral is crucial for mastering integration techniques. We'll explore the solution step-by-step, employing trigonometric substitution to simplify the expression and arrive at the final solution.
Understanding the Problem and Choosing a Strategy
The integral we're tackling is:
∫ 1/(1 + x²)^(3/2) dx
Direct integration is not immediately apparent. The presence of (1 + x²) suggests a trigonometric substitution might be the most efficient approach. Specifically, we'll utilize the substitution x = tan(θ). This substitution is particularly useful when dealing with expressions involving the square root of (1 + x²).
Step-by-Step Solution Using Trigonometric Substitution
-
Substitution: Let x = tan(θ). This implies dx = sec²(θ) dθ.
-
Substituting into the Integral: Substitute x and dx into the original integral:
∫ 1/(1 + tan²(θ))^(3/2) * sec²(θ) dθ
- Trigonometric Identity: Recall the Pythagorean identity: 1 + tan²(θ) = sec²(θ). Substitute this into the integral:
∫ 1/(sec²(θ))^(3/2) * sec²(θ) dθ = ∫ 1/sec³(θ) * sec²(θ) dθ
- Simplification: Simplify the expression:
∫ 1/sec(θ) dθ = ∫ cos(θ) dθ
- Integration: Integrate cos(θ):
∫ cos(θ) dθ = sin(θ) + C, where C is the constant of integration.
-
Back-Substitution: Now we need to express sin(θ) in terms of x. Since x = tan(θ), we can construct a right-angled triangle where the opposite side is x, the adjacent side is 1, and the hypotenuse is √(1 + x²). Therefore, sin(θ) = x / √(1 + x²).
-
Final Solution: Substitute this back into our result:
sin(θ) + C = x / √(1 + x²) + C
Therefore, the indefinite integral of 1/(1 + x²)^(3/2) is x / √(1 + x²) + C.
Applying the Solution to Definite Integrals
To solve a definite integral, you would evaluate this expression at the upper and lower limits of integration and subtract the results. For example, if you were asked to find the definite integral from 0 to 1, you would calculate:
[x / √(1 + x²) ] from 0 to 1 = (1 / √2) - 0 = 1/√2
Conclusion
This comprehensive guide demonstrates how to solve the integral of 1/(1 + x²)^(3/2) using trigonometric substitution. This technique is a powerful tool for tackling integrals involving expressions containing √(1 + x²), √(1 - x²), and √(x² - 1). Remember to always carefully choose your substitution and be mindful of trigonometric identities to successfully navigate these types of integration problems. Mastering this method is a significant step towards advanced calculus proficiency.
Latest Posts
Latest Posts
-
Why Do Cats Meow At The Door
Jun 08, 2025
-
What Does It Mean When A Dog Licks His Lips
Jun 08, 2025
-
How To Hang A Picture On A Brick Wall
Jun 08, 2025
-
How To Drop A Pin With Android
Jun 08, 2025
-
Can You Bring Shampoo In Checked Luggage
Jun 08, 2025
Related Post
Thank you for visiting our website which covers about Integral Of 1 1 X 2 3 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.