Integral Of X 2 X 2 1
Kalali
May 29, 2025 · 2 min read
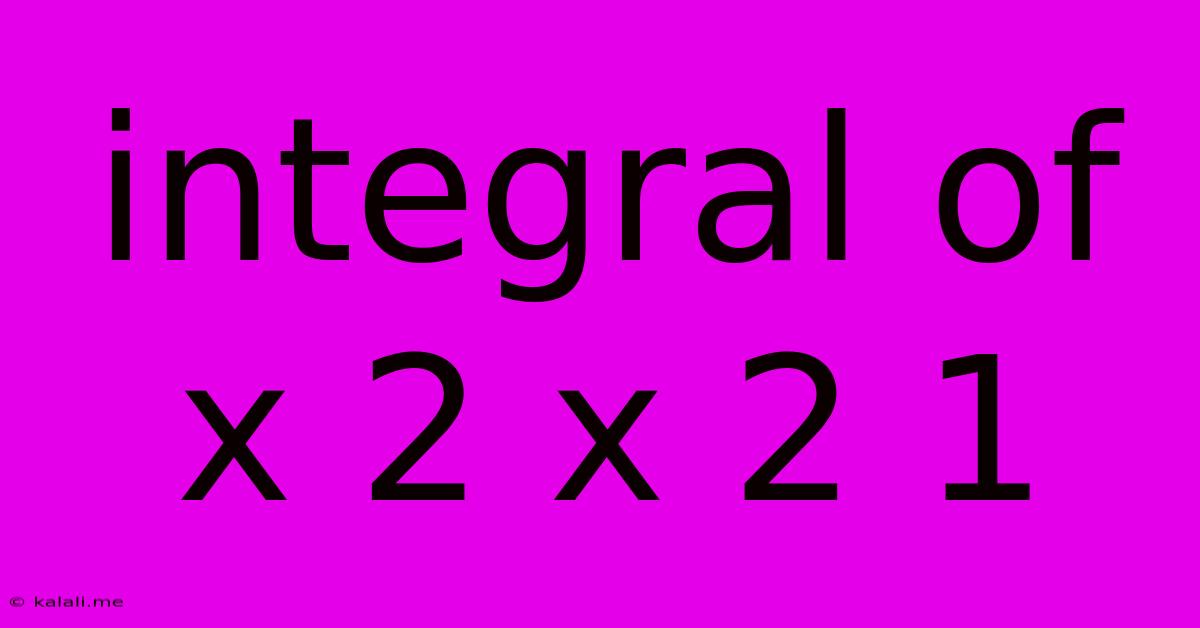
Table of Contents
Solving the Integral of x²/(x²+1)
This article will guide you through the process of solving the indefinite integral of x²/(x²+1). This integral might seem daunting at first, but with the right approach, it becomes quite manageable. We'll explore a straightforward method using polynomial long division and then briefly touch upon an alternative approach using trigonometric substitution. This approach is ideal for beginners and demonstrates a fundamental technique applicable to a range of integration problems.
Understanding the Problem:
We aim to find the indefinite integral: ∫x²/(x²+1) dx. This integral is not immediately solvable using basic integration rules. However, we can simplify the integrand using polynomial long division.
Method 1: Polynomial Long Division
The first step is to perform polynomial long division to simplify the integrand. Dividing x² by (x²+1), we get:
1
x²+1 | x² + 0x + 0
-x² -1
-------
-1
This division reveals that x²/(x²+1) = 1 - 1/(x²+1). Substituting this back into our integral, we obtain:
∫x²/(x²+1) dx = ∫[1 - 1/(x²+1)] dx
Now, we can integrate term by term:
∫1 dx = x + C₁ (where C₁ is the constant of integration)
∫1/(x²+1) dx = arctan(x) + C₂ (where C₂ is the constant of integration)
Therefore, the solution to the integral is:
∫x²/(x²+1) dx = x - arctan(x) + C (where C = C₁ + C₂ is the constant of integration)
Method 2: Trigonometric Substitution (Brief Overview)
While polynomial long division is the more straightforward approach for this particular integral, it's worth mentioning that trigonometric substitution is another viable method. This involves substituting x = tan(θ), which then transforms the integral into a trigonometric integral solvable using trigonometric identities. This method can be more complex and is generally preferred for integrals involving expressions like √(a² - x²), √(a² + x²), or √(x² - a²). For this specific problem, polynomial long division is significantly simpler.
Key Points to Remember:
- Polynomial long division: A powerful technique for simplifying rational functions before integration.
- Term-by-term integration: Allows us to break down complex integrals into simpler, manageable parts.
- Constants of integration: Always remember to include the constant of integration (+C) in indefinite integrals.
- Choosing the right method: Consider the structure of the integrand when deciding on the best integration technique.
Conclusion:
This article demonstrated a clear and concise method for solving the integral of x²/(x²+1) dx. By using polynomial long division, we effectively simplified the integrand, enabling us to easily integrate each term. While alternative methods exist, such as trigonometric substitution, the approach detailed here provides a straightforward and efficient solution for this particular problem. Understanding these techniques will equip you to tackle similar integration problems with confidence.
Latest Posts
Latest Posts
-
How To Best Store Api Keys In Docker Container
May 30, 2025
-
How Long Is Cooked Pork Good In Refrigerator
May 30, 2025
-
How Can I Get Candle Wax Out Of Carpet
May 30, 2025
-
How To Alt F4 On Mac
May 30, 2025
-
How To Bring The Thieves Guild To Its Former Glory
May 30, 2025
Related Post
Thank you for visiting our website which covers about Integral Of X 2 X 2 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.