Integration Of X 2 1 X 4 1
Kalali
Jun 08, 2025 · 2 min read
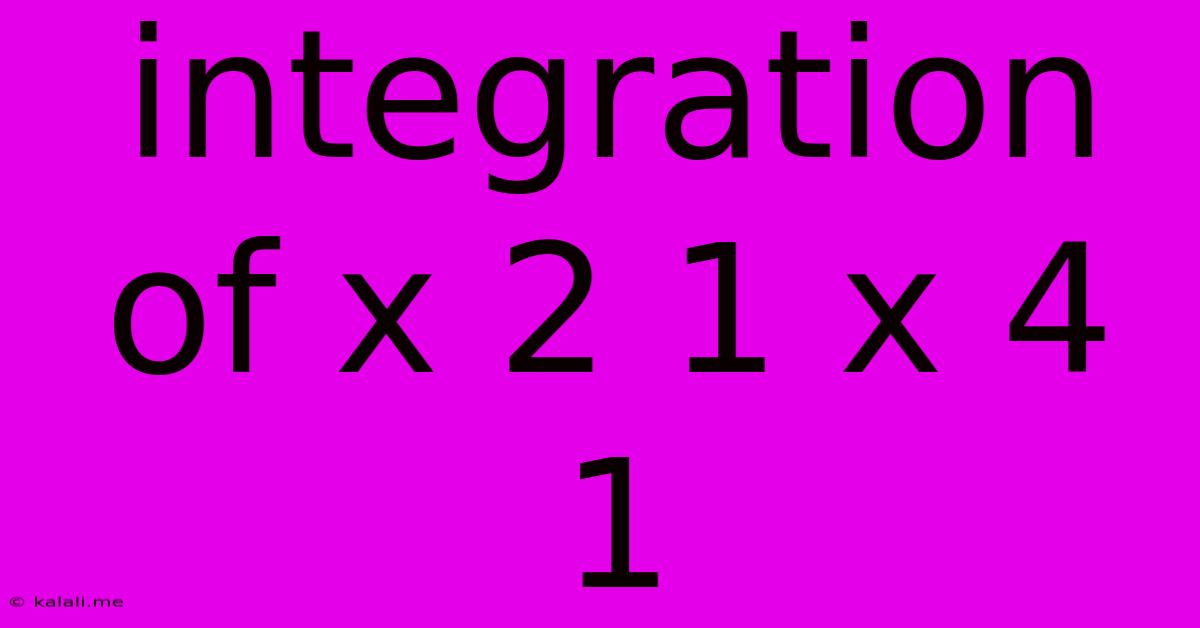
Table of Contents
Integrating (x² + 1) / (x⁴ + 1)
This article explores the integration of the rational function (x² + 1) / (x⁴ + 1). This seemingly simple integral presents a fascinating challenge, requiring a clever approach to solve. We'll break down the solution methodically, highlighting key techniques and concepts in calculus. Understanding this integration process will enhance your skills in manipulating rational functions and applying advanced integration techniques.
Understanding the Challenge
The immediate hurdle is the denominator, x⁴ + 1. This quartic polynomial isn't easily factorable using standard methods. Direct substitution or simple u-substitution won't work here. We need a more sophisticated strategy.
Strategy: Partial Fraction Decomposition
The key to solving this integral lies in partial fraction decomposition. However, before we can decompose the fraction, we need to factor the denominator. We can factor x⁴ + 1 using complex numbers, but a more practical approach for real-valued integration involves a clever manipulation.
Let's rewrite x⁴ + 1 as a difference of squares:
x⁴ + 1 = x⁴ + 2x² + 1 - 2x² = (x² + 1)² - (√2x)²
Now, we can use the difference of squares factorization again:
x⁴ + 1 = (x² + 1 - √2x)(x² + 1 + √2x)
Now that we have factored the denominator, we can proceed with partial fraction decomposition. The general form of the decomposition will be:
(x² + 1) / (x⁴ + 1) = (Ax + B) / (x² + 1 - √2x) + (Cx + D) / (x² + 1 + √2x)
Solving for A, B, C, and D
Finding the values of A, B, C, and D involves a bit of algebraic manipulation. We would multiply both sides by (x² + 1 - √2x)(x² + 1 + √2x), expand, and then equate the coefficients of the corresponding powers of x. This process is quite lengthy and involves solving a system of four linear equations. While the process is straightforward, it's best handled with a computer algebra system (CAS) or a symbolic mathematics program.
The Final Integral
Once we have determined A, B, C, and D, we are left with integrating two fractions of the form (ax + b) / (x² + cx + d). These integrals can be solved using a combination of substitution and standard integral formulas. Specifically, we can use the substitution u = x² + cx + d. The 'du' will contain an 'x dx' term allowing for a straightforward substitution. The resulting integral would involve logarithmic and arctangent functions.
Conclusion: A Multi-Step Process
The integration of (x² + 1) / (x⁴ + 1) is not a simple one. It requires a deep understanding of factoring techniques, partial fraction decomposition, and handling integrals with quadratic denominators. While the algebraic manipulation can be intricate, the underlying concepts are fundamental to advanced calculus. Remember to leverage computational tools to aid in the algebraic steps, focusing on understanding the methodology and the application of integration techniques. The final result will be a rather complex expression involving logarithmic and arctangent functions. The precise result heavily relies on the correct determination of A, B, C, and D from the partial fraction decomposition.
Latest Posts
Latest Posts
-
How To Remove Sewer Smell In Bathroom
Jun 08, 2025
-
How To Change Preview Of M4a File Mac
Jun 08, 2025
-
Hvac Compressor Fan Blowing But Compressor Not Working
Jun 08, 2025
-
How To Get Out Of Jail Monopoly
Jun 08, 2025
-
Thou Shalt Have No Other Gods Before
Jun 08, 2025
Related Post
Thank you for visiting our website which covers about Integration Of X 2 1 X 4 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.