Is 9 12 15 A Right Triangle
Kalali
Apr 01, 2025 · 6 min read
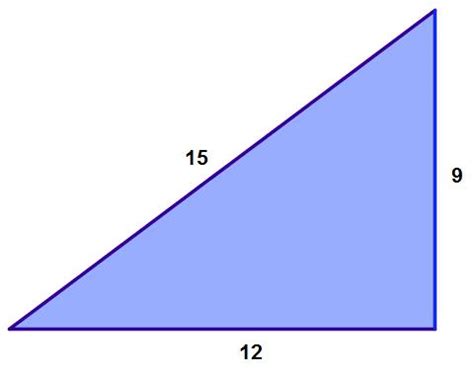
Table of Contents
Is 9-12-15 a Right Triangle? Exploring the Pythagorean Theorem and its Applications
Determining whether a triangle is a right-angled triangle is a fundamental concept in geometry, with widespread applications in various fields. This article delves deep into the question: "Is a triangle with sides 9, 12, and 15 a right triangle?" We'll explore the Pythagorean theorem, its proof, and demonstrate how to apply it to solve this problem and other similar geometrical challenges. We'll also examine real-world applications and discuss some common misconceptions.
Understanding the Pythagorean Theorem
The Pythagorean theorem is a cornerstone of Euclidean geometry, stating that in a right-angled triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides (called legs or cathetus). Mathematically, this is expressed as:
a² + b² = c²
where:
- a and b are the lengths of the two shorter sides (legs) of the right-angled triangle.
- c is the length of the hypotenuse (the longest side).
This theorem provides a straightforward method to determine if a triangle is a right-angled triangle, given the lengths of its sides. If the equation holds true, then the triangle is a right-angled triangle. If not, it's not.
Proving the Pythagorean Theorem
There are numerous ways to prove the Pythagorean theorem, ranging from simple geometric demonstrations to more complex algebraic proofs. One popular and visually intuitive proof involves using similar triangles. Consider a right-angled triangle with legs 'a' and 'b', and hypotenuse 'c'. Draw an altitude from the right angle to the hypotenuse, dividing the triangle into two smaller, similar triangles. Through ratios of corresponding sides in these similar triangles, and some algebraic manipulation, one can derive the Pythagorean theorem.
Another classic proof utilizes the rearrangement of squares. Consider constructing squares on each side of the right-angled triangle. By cleverly manipulating and rearranging the areas within these squares, one can demonstrate that the area of the square on the hypotenuse is indeed equal to the sum of the areas of the squares on the other two sides. This visual proof makes the theorem readily understandable.
Applying the Theorem to the 9-12-15 Triangle
Now let's apply the Pythagorean theorem to determine if the triangle with sides 9, 12, and 15 is a right-angled triangle. We need to identify the longest side, which is 15, so this will be our hypotenuse (c). The other two sides, 9 and 12, will be 'a' and 'b'.
Let's plug these values into the equation:
9² + 12² = 15²
81 + 144 = 225
225 = 225
The equation holds true! Therefore, a triangle with sides of length 9, 12, and 15 is indeed a right-angled triangle.
Identifying Right Triangles: A Systematic Approach
When determining if a triangle is a right triangle, always follow these steps:
- Identify the longest side: This side is the potential hypotenuse.
- Apply the Pythagorean Theorem: Substitute the values of the sides into the equation a² + b² = c².
- Evaluate the equation: If the equation is true, it's a right triangle; otherwise, it's not.
Remember, the order of 'a' and 'b' doesn't matter, as addition is commutative (a + b = b + a). However, it's crucial to correctly identify the hypotenuse ('c') as the longest side.
Beyond the 9-12-15 Triangle: Pythagorean Triples
The set of numbers (9, 12, 15) is an example of a Pythagorean triple – a set of three positive integers that satisfy the Pythagorean theorem. These triples represent the sides of right-angled triangles with integer side lengths. Other well-known Pythagorean triples include (3, 4, 5) and (5, 12, 13). Note that any multiple of a Pythagorean triple also forms a Pythagorean triple (e.g., multiplying (3, 4, 5) by 3 yields (9, 12, 15)).
The study of Pythagorean triples has fascinated mathematicians for centuries, leading to explorations in number theory and algebra. Finding new Pythagorean triples and understanding their properties remain active areas of mathematical research.
Real-World Applications of the Pythagorean Theorem
The Pythagorean theorem isn't just a theoretical concept; it has numerous practical applications in various fields:
- Construction and Engineering: Calculating distances, determining the correct angles for building structures, and ensuring stability in buildings and bridges.
- Navigation: Determining distances and bearings, particularly in surveying and geographical mapping.
- Computer Graphics: Creating realistic three-dimensional images and animations by accurately calculating distances and positions of objects.
- Physics: Calculating velocities and trajectories in projectile motion, particularly in scenarios involving right-angled paths.
- Everyday Life: Estimating distances, measuring diagonals, and solving various practical geometry problems.
Understanding and applying the Pythagorean theorem allows for precise measurements and calculations in many real-world situations.
Common Misconceptions about the Pythagorean Theorem
Despite its straightforward nature, some common misconceptions surrounding the Pythagorean theorem exist:
- Only applicable to right-angled triangles: The Pythagorean theorem specifically applies only to right-angled triangles. It doesn't hold true for other types of triangles (acute or obtuse).
- The longest side is always 'c': While the longest side is always the hypotenuse, accurately identifying the hypotenuse is essential for correctly applying the theorem.
- Units are unimportant: The units of measurement (meters, feet, centimeters, etc.) must be consistent throughout the equation. Mixing units will lead to incorrect results.
Understanding and avoiding these misconceptions is crucial for accurately applying the Pythagorean theorem.
Extending the Knowledge: Converse of the Pythagorean Theorem
The converse of the Pythagorean theorem is equally important. It states that if the square of the longest side of a triangle is equal to the sum of the squares of the other two sides, then the triangle is a right-angled triangle. This provides a method to prove that a given triangle is right-angled, even without prior knowledge of its angles. Our demonstration with the 9-12-15 triangle perfectly illustrates this converse.
Conclusion: The Significance of the 9-12-15 Triangle
The 9-12-15 triangle serves as an excellent example to solidify our understanding of the Pythagorean theorem and its applications. It's a simple yet powerful demonstration of a fundamental concept in geometry, highlighting the theorem's utility in both theoretical and practical contexts. By understanding this theorem and its implications, we can solve numerous geometrical problems and appreciate its widespread importance across various disciplines. The 9-12-15 triangle, a simple multiple of the fundamental (3, 4, 5) triple, provides a readily accessible and easily understood case study for mastering this essential mathematical concept. Remember to always meticulously check your calculations and ensure a thorough understanding of the theorem's underlying principles.
Latest Posts
Latest Posts
-
Describe The Cross Section Of The Rectangular Prism
Apr 02, 2025
-
7 Liters Is How Many Gallons
Apr 02, 2025
-
Is Baking Soda A Compound Element Or Mixture
Apr 02, 2025
-
What Is 177 Minutes In Hours And Minutes
Apr 02, 2025
-
Cuanto Es El 20 Por Ciento De 20
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Is 9 12 15 A Right Triangle . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
