Is Square Root Of 7 A Rational Number
Kalali
Apr 24, 2025 · 5 min read
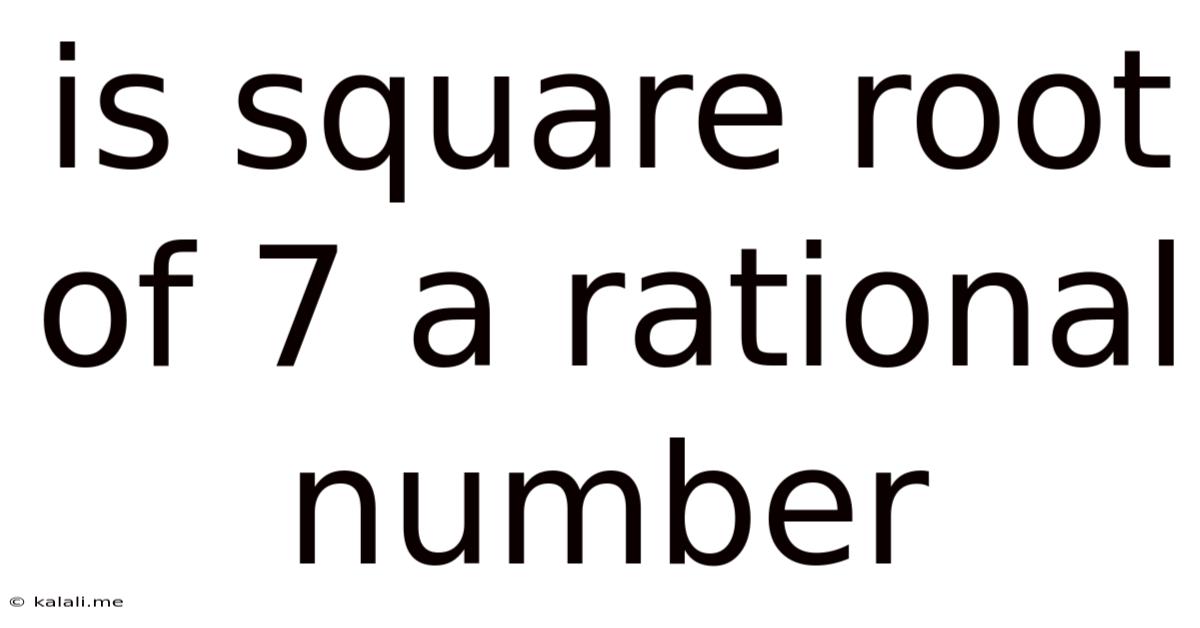
Table of Contents
Is the Square Root of 7 a Rational Number? A Deep Dive into Irrationality
The question of whether the square root of 7 is a rational number is a fundamental concept in mathematics, touching upon the core distinctions between rational and irrational numbers. This article will explore this question in detail, providing a comprehensive understanding not just of the answer, but also of the underlying mathematical principles involved. We'll delve into definitions, proofs, and explore related concepts to solidify your grasp of this important topic. Understanding this concept is crucial for anyone studying algebra, number theory, and even advanced mathematical fields.
What are Rational and Irrational Numbers?
Before we tackle the square root of 7 specifically, let's define our terms. Rational numbers are numbers that can be expressed as a fraction p/q, where p and q are integers, and q is not equal to zero. Think of it as any number that can be perfectly represented as a ratio of two whole numbers. Examples include 1/2, 3/4, -5/2, and even whole numbers like 7 (which can be expressed as 7/1). These numbers, when expressed in decimal form, either terminate (like 0.5) or repeat in a predictable pattern (like 1/3 = 0.333...).
Irrational numbers, on the other hand, cannot be expressed as a simple fraction of two integers. Their decimal representations are non-terminating and non-repeating. Famous examples include π (pi), approximately 3.14159..., and e (Euler's number), approximately 2.71828..., both of which have infinite, non-repeating decimal expansions. The square roots of many numbers also fall into this category.
Proof: The Square Root of 7 is Irrational
Now, let's address the main question: Is √7 a rational number? The answer is no, and we can prove this using a method called proof by contradiction. This method assumes the opposite of what we want to prove and then shows that this assumption leads to a contradiction.
1. Assume √7 is Rational:
Let's assume, for the sake of contradiction, that √7 is a rational number. This means it can be expressed as a fraction p/q, where p and q are integers, q ≠ 0, and p and q are coprime (meaning they share no common factors other than 1). This coprime condition is crucial for the proof.
2. Square Both Sides:
Squaring both sides of the equation √7 = p/q, we get:
7 = p²/q²
3. Rearrange the Equation:
Rearranging the equation, we have:
7q² = p²
This equation tells us that p² is a multiple of 7. Since 7 is a prime number, this means that p itself must also be a multiple of 7 (a fundamental property of prime numbers). We can express this as:
p = 7k, where k is an integer.
4. Substitute and Simplify:
Substituting p = 7k back into the equation 7q² = p², we get:
7q² = (7k)²
7q² = 49k²
Dividing both sides by 7, we get:
q² = 7k²
This equation shows us that q² is also a multiple of 7, and therefore, q must also be a multiple of 7.
5. The Contradiction:
We've now shown that both p and q are multiples of 7. This directly contradicts our initial assumption that p and q are coprime (having no common factors other than 1). Since our initial assumption leads to a contradiction, the assumption must be false.
6. Conclusion:
Therefore, our initial assumption that √7 is rational must be false. This means that √7 is an irrational number.
Understanding the Proof: Key Concepts
This proof relies heavily on the properties of prime numbers and the concept of coprime integers. Understanding these concepts is crucial to grasping the logic of the proof. Let's break them down further:
-
Prime Numbers: A prime number is a whole number greater than 1 that has only two divisors: 1 and itself. Examples include 2, 3, 5, 7, 11, and so on. A crucial property used in the proof is that if a prime number divides a square, it must also divide the original number.
-
Coprime Integers: Two integers are coprime if their greatest common divisor (GCD) is 1. In simpler terms, they share no common factors other than 1. This condition is essential in the proof because it allows us to establish the contradiction. If p and q were not coprime, we couldn't reach the contradictory conclusion.
Extending the Concept: Other Irrational Square Roots
The method used to prove the irrationality of √7 can be generalized to prove the irrationality of the square root of any non-perfect square. A perfect square is a number that can be obtained by squaring an integer (e.g., 4, 9, 16, 25, etc.). The square root of any positive integer that is not a perfect square will always be irrational. This includes numbers like √2, √3, √5, √6, √8, and countless others. The proof would follow a similar structure, replacing 7 with the non-perfect square in question.
Practical Implications and Applications
While the concept of irrational numbers might seem purely theoretical, it has significant practical implications in various fields:
-
Geometry: Irrational numbers are fundamental in geometry, appearing in calculations involving circles (π), triangles (various trigonometric functions), and other geometric shapes.
-
Physics: Many physical constants and equations involve irrational numbers, such as the gravitational constant and equations describing wave phenomena.
-
Computer Science: Approximating irrational numbers is a critical aspect of computer science, as computers work with finite precision. Algorithms are designed to handle these approximations efficiently and minimize errors.
-
Engineering: Calculations in engineering often involve irrational numbers, requiring careful consideration of precision and approximation techniques.
Conclusion: Embracing the Irrational
The square root of 7, along with many other square roots of non-perfect squares, belongs to the fascinating world of irrational numbers. While they cannot be expressed as simple fractions, their existence is fundamental to mathematics and has profound consequences across various scientific disciplines. Understanding the proof of their irrationality solidifies your comprehension of fundamental mathematical concepts and their implications in a wider context. The seemingly simple question of whether √7 is rational opens a door to a deeper understanding of the number system and its intricacies. The proof presented provides a clear and concise demonstration of mathematical reasoning, highlighting the power of proof by contradiction. The concepts explored here are building blocks for more advanced mathematical studies and demonstrate the beauty and elegance of mathematical logic.
Latest Posts
Latest Posts
-
75 Cm Equal How Many Inches
Apr 24, 2025
-
32 Feet Is How Many Inches
Apr 24, 2025
-
Cuanto Es 1 78 M En Pies
Apr 24, 2025
-
70 Is What Percent Of 56
Apr 24, 2025
-
Cuanto Es 70 Centimetros En Pulgadas
Apr 24, 2025
Related Post
Thank you for visiting our website which covers about Is Square Root Of 7 A Rational Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.