Least Common Multiple Of 6 And 5
Kalali
Apr 06, 2025 · 5 min read
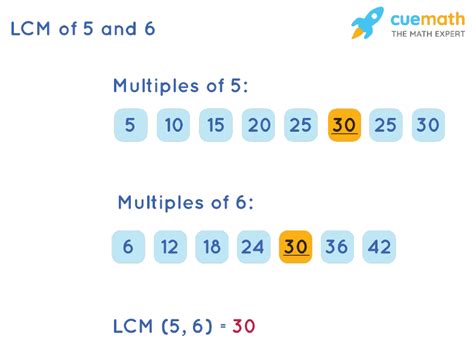
Table of Contents
Finding the Least Common Multiple (LCM) of 6 and 5: A Deep Dive
The least common multiple (LCM) is a fundamental concept in mathematics, particularly in number theory and algebra. Understanding how to find the LCM is crucial for solving various mathematical problems, from simplifying fractions to solving equations. This article will delve deep into finding the LCM of 6 and 5, exploring multiple methods and illustrating the broader applications of this concept. We’ll also touch upon the relationship between LCM and greatest common divisor (GCD), showcasing their interconnectedness.
Understanding Least Common Multiple (LCM)
Before we tackle the specific case of 6 and 5, let's establish a clear understanding of what LCM actually means. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that contains all the original numbers as factors.
For example, consider the numbers 2 and 3. The multiples of 2 are 2, 4, 6, 8, 10, 12… and the multiples of 3 are 3, 6, 9, 12, 15… The common multiples of 2 and 3 are 6, 12, 18… The least common multiple is 6.
Method 1: Listing Multiples
The most straightforward method to find the LCM is by listing the multiples of each number until you find the smallest common multiple. Let's apply this to 6 and 5:
Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60…
Multiples of 5: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60…
By comparing the lists, we can see that the smallest number appearing in both lists is 30. Therefore, the LCM of 6 and 5 is 30.
This method is simple and intuitive, particularly for smaller numbers. However, for larger numbers, listing multiples can become cumbersome and time-consuming. This highlights the need for more efficient methods.
Method 2: Prime Factorization
A more efficient and elegant method involves using prime factorization. Prime factorization is the process of expressing a number as a product of its prime factors. Let's break down 6 and 5 into their prime factors:
- 6 = 2 x 3
- 5 = 5 (5 is a prime number)
Once we have the prime factorization, we find the LCM by taking the highest power of each prime factor present in the factorizations and multiplying them together.
In this case, the prime factors are 2, 3, and 5. The highest power of 2 is 2¹, the highest power of 3 is 3¹, and the highest power of 5 is 5¹. Therefore, the LCM is:
LCM(6, 5) = 2 x 3 x 5 = 30
This method is significantly faster and more efficient than listing multiples, especially when dealing with larger numbers. It provides a systematic approach that avoids the trial-and-error nature of the listing method.
Method 3: Using the Formula Relating LCM and GCD
The least common multiple (LCM) and the greatest common divisor (GCD) are intimately related. There's a formula that elegantly connects them:
LCM(a, b) x GCD(a, b) = a x b
where 'a' and 'b' are the two numbers.
First, let's find the GCD of 6 and 5. The greatest common divisor is the largest number that divides both 6 and 5 without leaving a remainder. In this case, the only common divisor of 6 and 5 is 1. Therefore, GCD(6, 5) = 1.
Now, we can use the formula:
LCM(6, 5) x GCD(6, 5) = 6 x 5
LCM(6, 5) x 1 = 30
LCM(6, 5) = 30
This method demonstrates the inherent relationship between LCM and GCD. Knowing one allows you to easily calculate the other. This method is particularly useful when dealing with numbers where finding the GCD is relatively straightforward.
Applications of LCM
The concept of LCM finds widespread applications in various mathematical and real-world scenarios:
1. Fraction Addition and Subtraction:
Finding a common denominator when adding or subtracting fractions requires finding the LCM of the denominators. For instance, to add 1/6 and 1/5, you would find the LCM of 6 and 5 (which is 30), and then convert the fractions to have a common denominator of 30 before adding them.
2. Scheduling Problems:
LCM is frequently used in scheduling problems. Imagine two buses departing from the same station at different intervals. The LCM of their departure intervals will determine when both buses will depart simultaneously again.
3. Cyclic Patterns:
LCM helps to identify when cyclic patterns will coincide. For instance, if two events occur in cycles of 6 and 5 units of time, the LCM will indicate when both events will occur simultaneously.
4. Modular Arithmetic:
LCM plays a crucial role in modular arithmetic, a branch of number theory that deals with remainders after division.
Expanding on the Concept: LCM of More Than Two Numbers
The methods discussed above can be extended to find the LCM of more than two numbers. For the prime factorization method, you would simply find the prime factorization of each number, and then take the highest power of each prime factor present across all the factorizations. For the listing method, the process becomes more complex, requiring the comparison of multiple lists of multiples.
For example, let's find the LCM of 6, 5, and 10:
- 6 = 2 x 3
- 5 = 5
- 10 = 2 x 5
The prime factors are 2, 3, and 5. The highest powers are 2¹, 3¹, and 5¹. Therefore:
LCM(6, 5, 10) = 2 x 3 x 5 = 30
Conclusion: Mastering LCM for Mathematical Proficiency
Understanding and mastering the concept of the least common multiple is an essential skill for anyone pursuing mathematics or related fields. This article has explored several methods for finding the LCM, emphasizing their strengths and weaknesses. Whether you choose to list multiples, use prime factorization, or leverage the relationship with the GCD, the core concept remains the same: identifying the smallest positive integer divisible by all the given integers. By understanding this fundamental concept and its various applications, you enhance your mathematical proficiency and problem-solving capabilities across diverse scenarios. Remember to practice these methods with different numbers to solidify your understanding and become proficient in calculating LCMs. The seemingly simple concept of the LCM of 6 and 5 serves as a gateway to understanding more complex mathematical principles and their real-world applications.
Latest Posts
Latest Posts
-
Concave Mirror Focal Length Positive Or Negative
Apr 09, 2025
-
What Is The Percent Of 2 25
Apr 09, 2025
-
If 10 Be Added To Four Times
Apr 09, 2025
-
Nine Is What Percent Of 25
Apr 09, 2025
-
What Is 63 Inches In Height
Apr 09, 2025
Related Post
Thank you for visiting our website which covers about Least Common Multiple Of 6 And 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.