Lowest Common Multiple Of 5 And 6
Kalali
Mar 26, 2025 · 5 min read
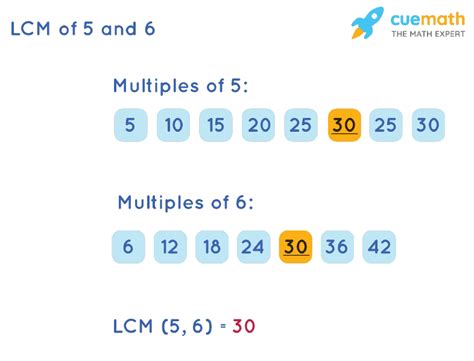
Table of Contents
Unveiling the Secrets of the Lowest Common Multiple: A Deep Dive into LCM(5,6)
Finding the lowest common multiple (LCM) might seem like a simple arithmetic task, but understanding its underlying principles unlocks a world of mathematical elegance and practical applications. This comprehensive guide delves into the concept of LCM, focusing specifically on LCM(5,6), providing multiple approaches to solving the problem and exploring its relevance in various mathematical contexts. We'll go beyond simply stating the answer; we'll explore why the answer is what it is and how this fundamental concept extends to more complex scenarios.
What is the Lowest Common Multiple (LCM)?
The Lowest Common Multiple (LCM) of two or more integers is the smallest positive integer that is a multiple of each of the integers. In simpler terms, it's the smallest number that both (or all) numbers divide into evenly. Understanding this definition is crucial to grasping the concept of LCM. For example, the LCM of 2 and 3 is 6, because 6 is the smallest number that is divisible by both 2 and 3.
Calculating LCM(5,6): Three Proven Methods
Let's now focus on finding the LCM of 5 and 6. We'll explore three distinct methods, each offering a unique perspective on this seemingly simple problem:
Method 1: Listing Multiples
This method is straightforward, especially for smaller numbers like 5 and 6. We simply list the multiples of each number until we find the smallest common multiple.
- Multiples of 5: 5, 10, 15, 20, 25, 30, 35...
- Multiples of 6: 6, 12, 18, 24, 30, 36...
By comparing the lists, we readily identify 30 as the smallest number present in both sequences. Therefore, LCM(5,6) = 30.
This method is effective for smaller numbers but becomes cumbersome and inefficient when dealing with larger numbers.
Method 2: Prime Factorization
This method is more sophisticated and scalable to larger numbers. It involves breaking down each number into its prime factors. The LCM is then constructed by taking the highest power of each prime factor present in the factorization of either number.
- Prime factorization of 5: 5 (5 is a prime number)
- Prime factorization of 6: 2 x 3
To find the LCM, we take the highest power of each prime factor: 2<sup>1</sup>, 3<sup>1</sup>, and 5<sup>1</sup>. Multiplying these together: 2 x 3 x 5 = 30. Therefore, LCM(5,6) = 30. This method provides a systematic approach that works reliably regardless of the size of the numbers.
Method 3: Using the Formula (LCM and GCD Relationship)
This method leverages the relationship between the Least Common Multiple (LCM) and the Greatest Common Divisor (GCD) of two numbers. The formula states:
LCM(a, b) x GCD(a, b) = a x b
where 'a' and 'b' are the two numbers.
First, we find the GCD (Greatest Common Divisor) of 5 and 6. The GCD is the largest number that divides both 5 and 6 without leaving a remainder. Since 5 and 6 share no common divisors other than 1, their GCD is 1.
Now, we can use the formula:
LCM(5, 6) x GCD(5, 6) = 5 x 6 LCM(5, 6) x 1 = 30 LCM(5, 6) = 30
This method is particularly useful when dealing with larger numbers where finding the GCD might be easier than directly calculating the LCM. The Euclidean algorithm is an efficient method for finding the GCD of larger numbers.
Real-World Applications of LCM
While LCM might seem like an abstract mathematical concept, it has practical applications in various fields:
Scheduling and Time Management:
Imagine you have two tasks: one that repeats every 5 days and another that repeats every 6 days. To find out when both tasks will coincide again, you need to find the LCM(5,6). The LCM of 5 and 6 is 30, meaning both tasks will coincide every 30 days. This concept is fundamental in scheduling appointments, production cycles, and even traffic light synchronization.
Fraction Operations:
LCM plays a crucial role when adding or subtracting fractions. To add fractions with different denominators, you need to find the LCM of the denominators and convert the fractions to have a common denominator before performing the addition or subtraction. For instance: 1/5 + 1/6 requires finding LCM(5,6) = 30 to get the common denominator.
Gear Ratios and Mechanical Engineering:
In mechanical engineering, gear ratios and the synchronization of rotating parts frequently rely on understanding LCM. Designing systems where multiple gears or rotating components work in harmony requires finding the LCM of their rotational speeds or cycle times.
Music and Rhythms:
The LCM concept finds application in music theory and the creation of harmonious rhythms. Understanding the LCM of different note durations or rhythmic patterns helps in composing complex and engaging musical pieces.
Extending the Concept: LCM of More Than Two Numbers
The principles of finding the LCM extend to situations involving more than two numbers. While the listing method becomes increasingly impractical, the prime factorization method and the GCD-based approach remain efficient. For instance, finding the LCM of 5, 6, and 10:
-
Prime Factorization:
- 5 = 5
- 6 = 2 x 3
- 10 = 2 x 5
-
LCM: Taking the highest power of each prime factor: 2<sup>1</sup> x 3<sup>1</sup> x 5<sup>1</sup> = 30
Therefore, LCM(5, 6, 10) = 30.
Conclusion: Mastering the LCM for Mathematical Proficiency
Understanding the lowest common multiple is not just about solving a specific arithmetic problem; it's about grasping a fundamental concept with far-reaching implications. Whether you're a student striving for mathematical proficiency, an engineer designing complex systems, or simply someone curious about the hidden connections within numbers, mastering the concept of LCM opens doors to a deeper appreciation of mathematics and its diverse applications. From scheduling tasks to solving complex fraction problems, the ability to calculate the LCM proves invaluable in diverse scenarios, emphasizing the importance of understanding this seemingly simple yet powerful mathematical concept. Remember the three methods detailed above – listing multiples, prime factorization, and the LCM/GCD relationship – to equip yourself with the tools to tackle LCM problems of any complexity.
Latest Posts
Latest Posts
-
How Many Oz Is In 100 Ml
Mar 29, 2025
-
How Many Ounces Is 1 Cup Of Sour Cream
Mar 29, 2025
-
How Much Feet Is 48 Inches
Mar 29, 2025
-
Are Alternate Interior Angles Always Congruent
Mar 29, 2025
-
What Percent Of 40 Is 38
Mar 29, 2025
Related Post
Thank you for visiting our website which covers about Lowest Common Multiple Of 5 And 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
