Negative Times A Negative Equals A
Kalali
May 31, 2025 · 2 min read
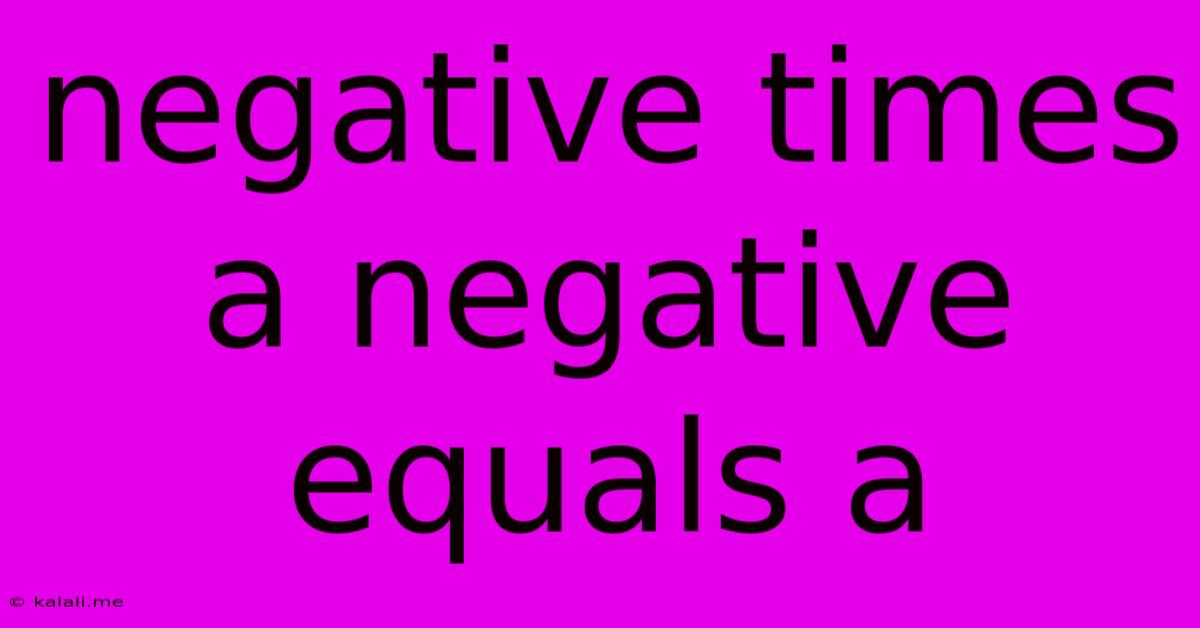
Table of Contents
Negative Times a Negative Equals a Positive: Understanding the Math Behind It
Why does a negative number multiplied by a negative number equal a positive number? This seemingly counterintuitive rule of mathematics often stumps students. This article will explore the reasoning behind this fundamental concept, providing a clear and intuitive explanation, along with practical examples. Understanding this principle is crucial for mastering algebra and beyond.
Understanding the Concept through Patterns:
One of the simplest ways to grasp this concept is by observing patterns in multiplication. Let's consider a series of multiplications involving decreasing negative numbers:
- 3 x (-3) = -9
- 2 x (-3) = -6
- 1 x (-3) = -3
- 0 x (-3) = 0
- -1 x (-3) = ?
Notice that as the first number decreases by one, the product increases by three. Following this pattern, -1 x (-3) must equal 3. This pattern visually demonstrates that multiplying a negative by a negative results in a positive.
The Number Line Approach:
Another useful approach is visualizing multiplication on a number line. Multiplication can be seen as repeated addition. For example, 3 x 2 means adding 2 three times (2 + 2 + 2 = 6).
Now, let's consider -3 x 2. This means adding -2 three times (-2 + -2 + -2 = -6).
What about -3 x -2? This can be interpreted as subtracting -2 three times. Subtracting a negative is the same as adding a positive. Therefore, -3 x -2 = 6.
Algebraic Explanation:
A more formal explanation utilizes the distributive property of multiplication. Let's consider the following expression:
(-a) * (-b)
We can rewrite -a as 0 - a. Substituting this into our expression:
(0 - a) * (-b)
Applying the distributive property:
0 * (-b) - a * (-b)
Since 0 multiplied by any number is 0, the expression simplifies to:
-a * (-b)
Now, we know that a negative multiplied by a positive is a negative. So:
- a * (-b) = ab
Therefore, (-a) * (-b) = ab, demonstrating that the product of two negative numbers is always positive.
Real-World Applications:
Understanding negative times a negative applies to various real-world scenarios. For instance, consider the concept of debt. If you have a debt (-$100) and you eliminate (-1) that debt, the net effect is an increase of $100 (+$100).
Conclusion:
The rule that a negative multiplied by a negative equals a positive might seem unconventional at first, but it's a consistent and logical consequence of the established rules of arithmetic. Understanding this concept through patterns, the number line, or algebraic proof provides a solid foundation for more advanced mathematical concepts. By grasping these explanations, you can conquer this mathematical hurdle and confidently navigate more complex calculations.
Latest Posts
Latest Posts
-
Can Quicktime Player Go Onto The Next Music File
Jun 01, 2025
-
When Can Kids Count To 10
Jun 01, 2025
-
Mixer Has Sends But No Returns
Jun 01, 2025
-
How To Make Cake From Brownie Mix
Jun 01, 2025
-
What Pase Is Normal Ameirican Home Power
Jun 01, 2025
Related Post
Thank you for visiting our website which covers about Negative Times A Negative Equals A . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.