Segment Of A Chord Definition Geometry
Kalali
Apr 06, 2025 · 6 min read
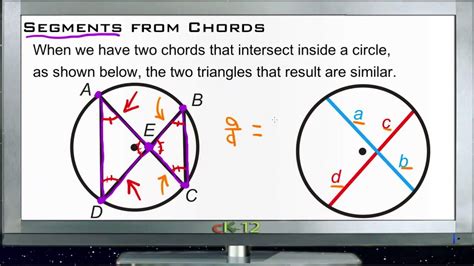
Table of Contents
Segment of a Chord: Definition, Properties, and Applications in Geometry
The seemingly simple concept of a chord segment in geometry opens a door to a rich tapestry of geometric relationships and applications. Understanding this concept thoroughly is crucial for anyone delving deeper into geometry, trigonometry, and even calculus. This comprehensive guide will explore the definition of a chord segment, delve into its properties, and illustrate its use in various geometric problems.
What is a Chord Segment? A Detailed Definition
Before we define a chord segment, let's establish the foundational concept of a chord. In a circle, a chord is a straight line segment whose endpoints both lie on the circumference of the circle. Think of it as a straight line connecting any two points on the circle's edge. The diameter of a circle, being the longest possible chord, is a special case.
Now, let's consider the chord segment. A chord segment is a portion of a chord that lies within a circle, specifically the portion between a point on the chord and a point on the circle's circumference where the chord intersects the circumference. It's important to understand that this is not simply half of a chord. The segment's starting point is always on the chord itself, not necessarily at its midpoint, and it terminates at a point on the circumference. The other end of the chord continues beyond the segment and also terminates on the circumference.
To visualize this: imagine a pizza. The diameter of the pizza is a chord. Now, imagine slicing a piece of pizza from the center outwards; the straight edge of the pizza slice, from the center to its edge, is not a chord segment. However, if you draw a chord anywhere across the pizza and then select a point on that chord, the distance from that point to the edge of the pizza along the chord represents a chord segment.
Key Properties of Chord Segments
Understanding the properties of chord segments is critical for solving geometric problems. While the concept appears simple, several crucial relationships emerge when dealing with chord segments within circles:
1. Relationship with the Radius and Diameter
A chord segment's length is directly related to the radius and diameter of the circle. While there's no single formula to directly calculate a chord segment's length based solely on the radius or diameter, it's implicitly connected. For example, if you know the distance from the center of the circle to the chord (which is perpendicular to the chord), you can use the Pythagorean theorem to calculate the length of the chord segment. Let's explore this further.
Consider a circle with center O and radius r. A chord AB intersects the circle at points A and B. Let M be the midpoint of the chord AB. Then, OM is perpendicular to AB. If we consider a point P on the chord AB, the length of the chord segment PB, for example, can be determined using the Pythagorean theorem within the triangle OMB.
2. Power of a Point Theorem
A powerful tool in solving geometric problems involving chords and chord segments is the Power of a Point Theorem. This theorem states that for any point P outside a circle, the product of the lengths of the two segments from P to the circle along any line through P is constant. This applies even if the line is tangent to the circle.
In the context of chord segments, this means that if you have two chords intersecting inside or outside a circle, the product of the lengths of the segments of one chord will equal the product of the lengths of the segments of the other chord. This relationship is invaluable when solving problems involving unknown chord segment lengths.
3. Chord Segment and Central Angle
The central angle subtended by a chord is directly related to the length of the chord. The larger the central angle, the longer the chord. However, the relationship is not linear. It involves trigonometric functions, specifically the sine function. The length of the chord can be expressed in terms of the radius and the central angle using the formula: Chord length = 2 * r * sin(θ/2), where 'r' is the radius and 'θ' is the central angle in radians.
This relationship helps establish a connection between the angular and linear measurements within the circle.
4. Intersecting Chords Theorem
When two chords intersect within a circle, the product of the lengths of the segments of one chord is equal to the product of the lengths of the segments of the other chord. This is another critical theorem relating chord segments. It provides a powerful algebraic relationship to solve for unknown chord segment lengths. This theorem is closely related to the Power of a Point Theorem.
Applications of Chord Segments in Geometry
The concepts of chords and chord segments are not merely theoretical exercises. They have numerous practical applications in various fields of geometry and beyond:
1. Solving Geometric Problems
Numerous geometry problems hinge on understanding and applying the properties of chord segments. Many problems involve finding unknown lengths of chords or segments, angles, or the radius of the circle. The Power of a Point Theorem and the Intersecting Chords Theorem are instrumental in solving these types of problems. For example, if you know the lengths of some chord segments and need to find the length of an unknown segment, you can utilize these theorems to establish equations and solve for the unknown value.
2. Trigonometry and Circular Functions
The relationships between chord lengths, radii, and central angles directly link to trigonometric functions. Calculating chord segment lengths often requires the application of sine, cosine, and tangent functions. The formula connecting the chord length, radius, and central angle is a prime example of this link.
3. Coordinate Geometry
Chord segments can be described using coordinate geometry. If you know the coordinates of the endpoints of a chord and a point on that chord, you can determine the length of the chord segment using the distance formula. The equation of a circle can also be used to find the intersection points of a chord and thus the length of the chord segments.
4. Applications in Physics and Engineering
The concept of chords and their segments finds applications in various fields of physics and engineering. For instance, understanding circular motion, analyzing the trajectory of projectiles, or designing circular structures often utilizes geometric principles that involve chord segments.
Advanced Concepts and Further Exploration
The study of chord segments extends beyond the basic definitions and properties. More advanced concepts include:
- Cyclic Quadrilaterals: The properties of chord segments play a crucial role in understanding cyclic quadrilaterals, which are quadrilaterals whose vertices all lie on a circle.
- Inscribed Angles: The relationship between inscribed angles and the chords that subtend them provides further insights into the geometry of circles.
- Apollonius' Theorem: This theorem, relating the lengths of medians and sides of a triangle, can be extended to scenarios involving chord segments.
Conclusion: The Significance of Chord Segments
The seemingly simple concept of a chord segment reveals a depth and complexity that extends throughout many areas of geometry. Mastering the definition, properties, and applications of chord segments provides a strong foundation for tackling more advanced geometric problems. By understanding the relationships between chord segments, radii, central angles, and other geometric elements, you unlock a powerful toolkit for solving a wide array of geometric challenges. The theorems and relationships discussed here are not merely abstract concepts but practical tools applicable in diverse fields. A thorough understanding of chord segments will enhance your skills in problem-solving and your appreciation for the elegance and interconnectedness of geometry.
Latest Posts
Latest Posts
-
Cuanto Es 5 5 Pies En Centimetros
Apr 08, 2025
-
11 Is What Percent Of 20
Apr 08, 2025
-
What Is 19 Degrees Fahrenheit In Celsius
Apr 08, 2025
-
How Many Oz In 1 4 Pound
Apr 08, 2025
-
How Many Hours Is 260 Minutes
Apr 08, 2025
Related Post
Thank you for visiting our website which covers about Segment Of A Chord Definition Geometry . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.