What Are The Factors Of 21
Kalali
Mar 28, 2025 · 6 min read
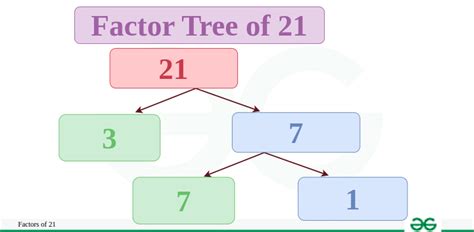
Table of Contents
What are the Factors of 21? A Deep Dive into Prime Factorization and Number Theory
The seemingly simple question, "What are the factors of 21?" opens a door to a fascinating world of number theory, prime factorization, and the fundamental building blocks of mathematics. While the immediate answer might seem straightforward, exploring this question allows us to delve into concepts crucial to understanding more complex mathematical ideas. This article will not only answer the question directly but also explore the broader mathematical context, explaining the concepts involved and their significance.
Understanding Factors
Before we pinpoint the factors of 21, let's define what a factor actually is. In mathematics, a factor (or divisor) of a number is an integer that divides that number exactly, leaving no remainder. For instance, if we divide 21 by one of its factors, the result will be a whole number.
Finding Factors: A Systematic Approach
There are several ways to find the factors of any given number. For smaller numbers like 21, a simple approach is to systematically test each integer, starting from 1, to see if it divides 21 without leaving a remainder.
Let's try this:
- 1: 21 divided by 1 is 21 (no remainder). Therefore, 1 is a factor.
- 2: 21 divided by 2 is 10 with a remainder of 1. Therefore, 2 is not a factor.
- 3: 21 divided by 3 is 7 (no remainder). Therefore, 3 is a factor.
- 4: 21 divided by 4 leaves a remainder.
- 5: 21 divided by 5 leaves a remainder.
- 6: 21 divided by 6 leaves a remainder.
- 7: 21 divided by 7 is 3 (no remainder). Therefore, 7 is a factor.
- Numbers greater than 7: We can stop here because any factor greater than 7 would necessarily have a corresponding factor less than 7, which we've already checked.
Therefore, the factors of 21 are 1, 3, 7, and 21.
Prime Factorization: The Building Blocks
The concept of prime factorization is central to understanding the factors of any number. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself. Examples include 2, 3, 5, 7, 11, and so on. Prime factorization involves expressing a number as a product of its prime factors. This representation is unique for every number (except for the order of the factors).
Prime Factorization of 21
To find the prime factorization of 21, we can use a factor tree. We start by finding any two factors of 21. We already know that 3 and 7 are factors:
21
/ \
3 7
Since both 3 and 7 are prime numbers, we have found the prime factorization of 21: 3 x 7. This means that 21 can only be expressed as the product of 3 and 7. This unique representation is fundamental in various areas of mathematics.
Divisibility Rules: Shortcuts and Efficiency
Understanding divisibility rules can significantly speed up the process of finding factors. Divisibility rules provide quick ways to determine if a number is divisible by a particular integer without performing long division.
Some useful divisibility rules include:
- Divisibility by 2: A number is divisible by 2 if its last digit is even (0, 2, 4, 6, or 8).
- Divisibility by 3: A number is divisible by 3 if the sum of its digits is divisible by 3. (For 21: 2 + 1 = 3, which is divisible by 3).
- Divisibility by 5: A number is divisible by 5 if its last digit is 0 or 5.
- Divisibility by 7: There's no single easy rule, but we can use repeated subtraction or other methods.
- Divisibility by 9: A number is divisible by 9 if the sum of its digits is divisible by 9.
- Divisibility by 11: A number is divisible by 11 if the alternating sum of its digits is divisible by 11.
Using these rules, we can quickly eliminate potential factors and focus on those that are more likely candidates.
Applications of Factors and Prime Factorization
The concepts of factors and prime factorization are not merely theoretical exercises. They have numerous applications in various fields, including:
1. Cryptography: Securing Information
Prime numbers and their properties are fundamental to modern cryptography. Many encryption algorithms rely heavily on the difficulty of factoring very large numbers into their prime components. The security of online transactions and sensitive data often depends on the computational complexity of prime factorization.
2. Modular Arithmetic: The Clock and Beyond
Modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" upon reaching a certain value, called the modulus. Factors and prime factorization play a crucial role in understanding the structure and properties of modular arithmetic, which has applications in cryptography, computer science, and various other fields.
3. Algebra and Polynomial Factoring
The concept of factoring extends beyond integers to polynomials in algebra. Factoring polynomials, similar to factoring integers, involves expressing a polynomial as a product of simpler polynomials. This is a fundamental technique in solving equations and simplifying expressions in algebra.
4. Number Theory Research: Exploring the Unknowns
Number theory, a branch of mathematics dedicated to the study of integers and their properties, extensively utilizes the concept of prime factorization. Many open problems in number theory, such as the Riemann Hypothesis, relate directly to the distribution and properties of prime numbers.
5. Computer Science Algorithms: Efficiency and Optimization
Many algorithms in computer science rely on efficient ways to find factors and perform prime factorization. The complexity of these algorithms determines the speed and efficiency of various computations. For instance, efficient algorithms for factoring are crucial for tasks like database searching and data compression.
Beyond the Basics: Exploring Further Concepts
The exploration of factors of 21 extends beyond finding its simple factors. We can delve into more advanced concepts like:
-
Greatest Common Divisor (GCD): Finding the largest number that divides two or more integers without leaving a remainder. For example, the GCD of 21 and 14 is 7.
-
Least Common Multiple (LCM): Finding the smallest number that is a multiple of two or more integers. For example, the LCM of 21 and 14 is 42.
-
Euler's Totient Function: This function counts the number of positive integers up to a given integer n that are relatively prime to n (meaning they share no common factors other than 1). This function has significant applications in number theory and cryptography.
-
Divisor Function: This function counts the number of divisors of a given integer. For 21, the divisor function would return 4 (because 21 has four divisors: 1, 3, 7, and 21).
Conclusion: The Significance of Simple Numbers
The seemingly trivial question of the factors of 21 unveils a world of rich mathematical concepts and their diverse applications. From understanding prime factorization to appreciating the power of divisibility rules and their role in cryptography and computer science, the journey from a simple number to a complex web of mathematical ideas demonstrates the beauty and intricacy inherent in number theory. This exploration serves not only as an answer to a specific question but also as a gateway to deeper understanding and appreciation of the fundamental building blocks of mathematics. The factors of 21—1, 3, 7, and 21—represent more than just divisors; they represent a key to unlocking a vast landscape of mathematical exploration.
Latest Posts
Latest Posts
-
How Much Is 64 Oz In Cups
Mar 31, 2025
-
What Is The Second Step In Dna Replication
Mar 31, 2025
-
220 C Is What In Fahrenheit
Mar 31, 2025
-
How Much Is 55 Cm In Inches
Mar 31, 2025
-
How Long It Takes To Boil Water
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about What Are The Factors Of 21 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
