What Divides An Angle Into Two Congruent Angles
Kalali
Mar 28, 2025 · 6 min read
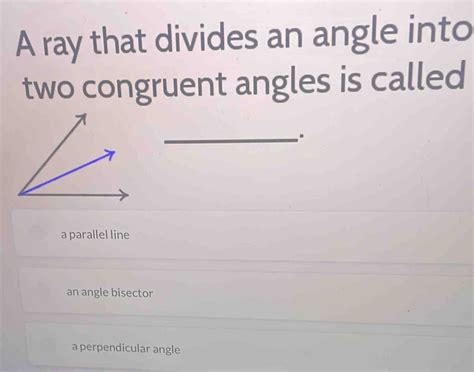
Table of Contents
What Divides an Angle into Two Congruent Angles? A Comprehensive Guide
Understanding how to bisect an angle is fundamental in geometry and has widespread applications in various fields. This comprehensive guide delves deep into the concept of angle bisectors, exploring their properties, construction methods, and practical applications. We will cover everything from the basic definition to advanced theorems and real-world examples.
Understanding Angles and Congruence
Before we dive into angle bisectors, let's refresh our understanding of angles and congruence.
What is an angle? An angle is formed by two rays that share a common endpoint, called the vertex. Angles are measured in degrees, with a full rotation being 360 degrees.
Types of Angles: We encounter various types of angles, including:
- Acute Angles: Angles measuring less than 90 degrees.
- Right Angles: Angles measuring exactly 90 degrees.
- Obtuse Angles: Angles measuring greater than 90 degrees but less than 180 degrees.
- Straight Angles: Angles measuring exactly 180 degrees (a straight line).
- Reflex Angles: Angles measuring greater than 180 degrees but less than 360 degrees.
What is Congruence? In geometry, two figures are congruent if they have the same size and shape. For angles, congruence means they have the same measure in degrees.
Defining the Angle Bisector
An angle bisector is a ray that divides an angle into two congruent angles. This means the bisector creates two smaller angles that are equal in measure. The ray originates from the vertex of the original angle and extends into the interior of the angle, perfectly splitting it in half.
Key Properties of an Angle Bisector:
- Equidistant from the Sides: Any point on the angle bisector is equidistant from the two sides of the original angle. This is a crucial property used in many geometric constructions and proofs.
- Unique: For any given angle, there is only one angle bisector.
Constructing an Angle Bisector
Constructing an angle bisector accurately is crucial for many geometric problems. The most common method involves using a compass and straightedge:
Steps to Construct an Angle Bisector:
-
Draw an Arc: Place the compass point on the vertex of the angle. Draw an arc that intersects both rays of the angle. Label the intersection points A and B.
-
Draw Two More Arcs: Place the compass point at A and draw an arc inside the angle. Without changing the compass width, place the compass point at B and draw another arc intersecting the first arc. Label the intersection point C.
-
Draw the Bisector: Draw a ray from the vertex of the angle through point C. This ray is the angle bisector. It divides the original angle into two congruent angles, ∠VAC and ∠VBC.
Why this Construction Works:
The construction works because of the properties of congruent triangles. By drawing equal arcs from A and B, we create two isosceles triangles (△AVC and △BVC). The equal distances ensure that AC = BC and that the triangles are congruent. Therefore, ∠VAC = ∠VBC, proving the ray VC bisects the angle.
Angle Bisector Theorem
The Angle Bisector Theorem describes the relationship between an angle bisector and the sides of a triangle. It states:
An angle bisector of a triangle divides the opposite side into segments that are proportional to the lengths of the other two sides.
Let's say we have a triangle △ABC, and ray AD bisects ∠BAC. The theorem states that:
AB/AC = BD/DC
This theorem is extremely useful in solving problems involving triangle proportions and unknown side lengths.
Applications of Angle Bisectors
Angle bisectors are not just a theoretical concept; they have many practical applications in various fields:
-
Architecture and Design: Architects and designers utilize angle bisectors to create symmetrical and balanced designs in buildings, landscapes, and interior spaces. Think of the perfectly symmetrical patterns found in many architectural marvels.
-
Engineering and Surveying: Angle bisectors are employed in surveying to accurately determine distances and angles, particularly when dealing with triangulation methods.
-
Computer Graphics and Animation: In computer-aided design (CAD) and animation, angle bisectors are used to create precise shapes and movements. Many software programs rely on geometric principles, including angle bisection, to build complex models.
-
Navigation and Cartography: Angle bisectors play a role in navigation systems, aiding in determining optimal routes and locations. This is especially relevant in situations requiring precise calculations of angles and distances.
-
Astronomy: While less direct, understanding angle bisection contributes to the ability to accurately measure and analyze angular distances between celestial bodies.
Advanced Concepts and Theorems related to Angle Bisectors
Beyond the basic concepts, several advanced theorems and properties further enhance our understanding of angle bisectors.
-
Incenter of a Triangle: The three angle bisectors of a triangle are concurrent, meaning they intersect at a single point. This point is called the incenter, and it is the center of the inscribed circle (incircle) of the triangle. The incircle is tangent to all three sides of the triangle.
-
Exterior Angle Bisectors: Similar to interior angle bisectors, exterior angle bisectors divide the exterior angle of a triangle into two congruent angles. The intersection of two exterior angle bisectors and one interior angle bisector creates interesting geometric properties.
Solving Problems Involving Angle Bisectors
Let's look at a few example problems that demonstrate the application of angle bisectors:
Problem 1: Given an angle of 120 degrees, construct its bisector using a compass and straightedge. Follow the steps outlined in the construction section above to achieve this.
Problem 2: In △ABC, AB = 6 cm, AC = 8 cm, and the angle bisector of ∠A intersects BC at point D. If BD = 4 cm, what is the length of DC? Use the Angle Bisector Theorem to solve this: 6/8 = 4/DC. Solving for DC gives us DC = 16/3 cm.
Problem 3: Prove that the angle bisectors of a triangle are concurrent. This requires a more formal geometric proof, utilizing properties of triangles and intersecting lines. The proof would demonstrate that the intersection point of any two angle bisectors is equidistant from the sides of the triangle, hence the third angle bisector must also pass through this point.
Conclusion
Understanding angle bisectors is a fundamental aspect of geometry with diverse applications across various fields. From basic constructions to advanced theorems, this guide offers a thorough exploration of the subject. Mastering the concepts and techniques related to angle bisectors is not just essential for academic success but also opens up doors to further exploration in more advanced geometric concepts and practical applications. The ability to visualize, construct, and solve problems involving angle bisectors significantly enhances problem-solving skills and mathematical intuition. Remember to practice regularly and explore further resources to solidify your understanding and unlock the vast potential of this essential geometric concept.
Latest Posts
Latest Posts
-
How Many Ounces Are In 8 Lb
Mar 31, 2025
-
Which Group Has The Highest Electronegativity
Mar 31, 2025
-
Cuanto Es 15 Pies En Centimetros
Mar 31, 2025
-
Lowest Common Multiple Of 14 And 6
Mar 31, 2025
-
9 Out Of 24 As A Percentage
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about What Divides An Angle Into Two Congruent Angles . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
