What Is -0.35 As A Fraction
Kalali
Apr 18, 2025 · 5 min read
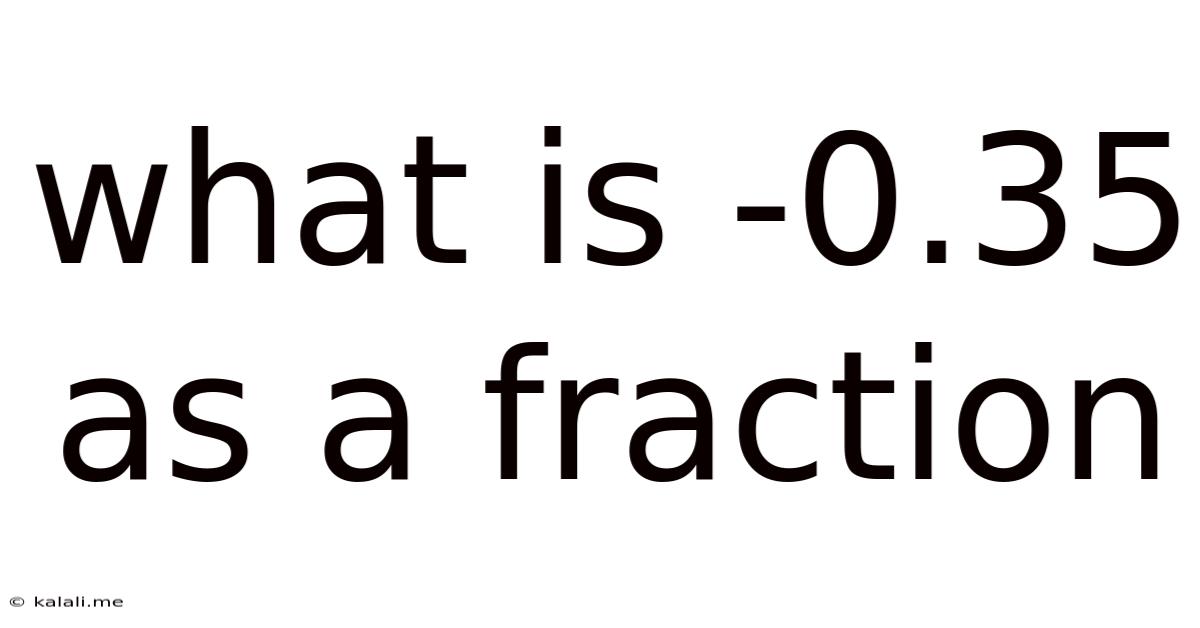
Table of Contents
Decoding -0.35: A Deep Dive into Fraction Conversion
What is -0.35 as a fraction? This seemingly simple question opens the door to a deeper understanding of decimal-to-fraction conversion, negative numbers, and the fundamental principles of mathematics. This comprehensive guide will not only answer the initial question but also equip you with the skills to tackle similar conversions with ease, solidifying your grasp of fractional representation. We'll explore various methods, address common pitfalls, and delve into the practical applications of understanding decimal-fraction equivalencies.
Understanding Decimal and Fraction Representation
Before we dive into the conversion of -0.35, it's crucial to understand the underlying concepts of decimals and fractions. Decimals represent numbers as parts of ten, hundred, thousand, and so on. The decimal point separates the whole number from the fractional part. Fractions, on the other hand, express numbers as a ratio of two integers: a numerator (the top number) and a denominator (the bottom number). Understanding the relationship between these two representations is key to performing accurate conversions.
Converting -0.35 to a Fraction: Step-by-Step Guide
The first step in converting -0.35 to a fraction is to ignore the negative sign for now. We'll address the negative aspect later. The decimal 0.35 can be read as "thirty-five hundredths." This directly translates to a fraction with a numerator of 35 and a denominator of 100:
35/100
Now, we need to simplify this fraction to its lowest terms. This involves finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it. The GCD of 35 and 100 is 5. Dividing both the numerator and the denominator by 5, we get:
35 ÷ 5 = 7 100 ÷ 5 = 20
Therefore, the simplified fraction is 7/20. Now, remember the negative sign we initially set aside? We simply add it back to the simplified fraction to obtain the final answer:
-7/20
This is the simplest form of the fraction representing -0.35.
Alternative Methods for Decimal to Fraction Conversion
While the above method is straightforward, several other approaches can be used to convert decimals to fractions, especially for more complex decimals.
Method 2: Using Place Value
This method relies on understanding the place value of each digit in the decimal. In 0.35, the 3 is in the tenths place, and the 5 is in the hundredths place. This can be written as:
(3 × 1/10) + (5 × 1/100) = 3/10 + 5/100
To add these fractions, we need a common denominator, which is 100. Therefore:
(30/100) + (5/100) = 35/100
This fraction can then be simplified as shown in the previous method, resulting in -7/20.
Method 3: Using Scientific Notation (for more complex decimals)
For decimals with many digits after the decimal point, scientific notation can simplify the conversion process. Let's consider a more complex example, -0.00375. This can be written in scientific notation as -3.75 x 10⁻³. Then, we convert 3.75 to a fraction:
3.75 = 375/100 = 15/4
Now, we substitute this back into the scientific notation:
-15/4 x 10⁻³ = -15/(4 x 10³) = -15/4000
Simplifying this fraction gives us -3/800. This method proves particularly useful when dealing with very small or very large decimals.
Common Mistakes to Avoid
Several common mistakes can arise when converting decimals to fractions:
- Forgetting the negative sign: Always remember to account for the negative sign in the decimal when converting it to a fraction.
- Incorrect simplification: Ensure you simplify the fraction to its lowest terms by finding the greatest common divisor of the numerator and denominator.
- Misunderstanding place value: Accurately identifying the place value of each digit in the decimal is crucial for correct conversion.
- Arithmetic errors: Double-check your calculations to minimize errors in addition, subtraction, multiplication, and division.
Practical Applications of Decimal-Fraction Conversion
Understanding decimal-fraction conversion is crucial in numerous practical applications across various fields:
- Engineering and Science: Precise measurements and calculations in engineering and scientific fields often require converting between decimals and fractions.
- Cooking and Baking: Recipes often use fractions for ingredient quantities, and understanding the decimal equivalent can be helpful.
- Finance: Calculations involving percentages and interest rates often require converting between decimals and fractions.
- Data Analysis: Working with data sets may involve converting decimals to fractions for better understanding and representation.
- Construction: Precise measurements in construction often require converting between decimals and fractions to ensure accuracy.
Expanding on the Concept of Negative Fractions
The presence of the negative sign in -0.35 and its fractional equivalent, -7/20, highlights the concept of negative numbers within the context of fractions. A negative fraction simply represents a negative quantity, just as a negative decimal does. It indicates a value less than zero. The rules for operating with negative fractions are consistent with the rules for operating with negative numbers in general. For example, adding a negative fraction is equivalent to subtracting a positive fraction.
Conclusion
Converting -0.35 to its fractional equivalent, -7/20, is a straightforward process once you understand the underlying principles of decimal and fraction representation. This seemingly simple conversion exemplifies the fundamental relationship between these two systems of numerical representation. Mastering this skill is invaluable, providing a solid foundation for tackling more complex mathematical problems across diverse fields. Remember the steps, avoid common pitfalls, and apply your knowledge to solve a wide range of decimal-to-fraction conversion problems. The ability to fluently translate between decimals and fractions is a vital skill for anyone seeking a deeper understanding of mathematics and its real-world applications.
Latest Posts
Latest Posts
-
3 5 Feet Is How Many Inches
Apr 19, 2025
-
3 Out Of 13 As A Percentage
Apr 19, 2025
-
Which Statement Describes An Atomic Nucleus
Apr 19, 2025
-
What Is A Factor Of 56
Apr 19, 2025
-
Least Common Multiple Of 9 And 10
Apr 19, 2025
Related Post
Thank you for visiting our website which covers about What Is -0.35 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.