What Is 1/50 As A Percent
Kalali
Apr 03, 2025 · 4 min read
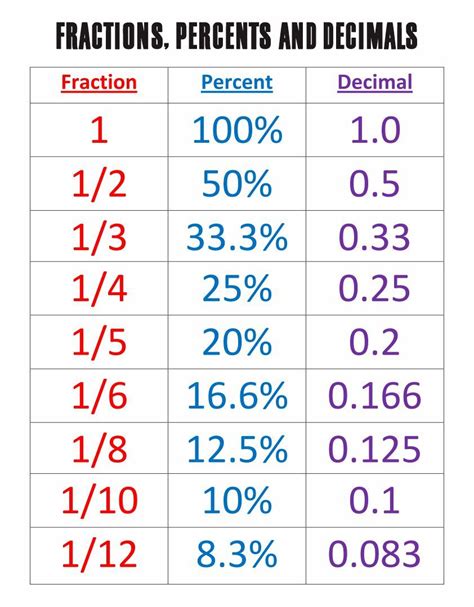
Table of Contents
What is 1/50 as a Percent? A Comprehensive Guide
Understanding fractions and their percentage equivalents is a fundamental skill in mathematics and has widespread applications in various fields, from everyday budgeting to complex financial calculations. This comprehensive guide delves deep into the conversion of fractions to percentages, specifically focusing on how to express 1/50 as a percentage. We'll explore the process step-by-step, discuss different methods, and highlight the practical significance of this conversion.
Understanding Fractions and Percentages
Before diving into the conversion of 1/50, let's establish a clear understanding of fractions and percentages.
Fractions: A fraction represents a part of a whole. It consists of two parts: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts you have, and the denominator indicates how many parts make up the whole. For instance, in the fraction 1/50, 1 is the numerator and 50 is the denominator. This means we have one part out of a total of fifty equal parts.
Percentages: A percentage is a way of expressing a number as a fraction of 100. The symbol "%" represents "per cent," meaning "out of one hundred." Percentages are widely used to express proportions, rates, and changes. For example, 25% means 25 out of 100, or 25/100.
Converting Fractions to Percentages: The Fundamental Method
The fundamental method for converting a fraction to a percentage involves two key steps:
- Convert the fraction to a decimal: Divide the numerator by the denominator.
- Multiply the decimal by 100: This converts the decimal to a percentage.
Let's apply this method to convert 1/50 to a percentage:
Step 1: Convert to a decimal:
1 ÷ 50 = 0.02
Step 2: Multiply by 100:
0.02 × 100 = 2
Therefore, 1/50 as a percentage is 2%.
Alternative Methods for Conversion
While the fundamental method is straightforward, other approaches can offer alternative perspectives and strengthen understanding.
Method 1: Using Equivalent Fractions:
We can create an equivalent fraction with a denominator of 100. To do this, we ask: what number multiplied by 50 equals 100? The answer is 2. Therefore, we multiply both the numerator and denominator of 1/50 by 2:
(1 × 2) / (50 × 2) = 2/100
Since 2/100 means 2 out of 100, this directly translates to 2%.
Method 2: Using Proportions:
We can set up a proportion to solve for the percentage:
1/50 = x/100
Cross-multiplying gives us:
50x = 100
Dividing both sides by 50:
x = 2
Thus, x represents the percentage, confirming that 1/50 is equal to 2%.
Practical Applications of 1/50 as a Percentage
The knowledge that 1/50 equals 2% has practical applications in diverse scenarios:
-
Finance: Calculating interest rates, discounts, or profit margins often involves working with percentages and fractions. Understanding this conversion allows for efficient calculations in financial planning and analysis. For example, a 2% discount on a $100 item represents a savings of $2.
-
Statistics: Many statistical analyses involve working with proportions and percentages. Representing data as percentages provides a clear and easily understandable way to communicate findings. Understanding 1/50 as 2% facilitates interpretation of data represented as fractions.
-
Everyday Life: Percentages are commonplace in everyday life – from calculating tips and sales tax to understanding survey results and interpreting data presented in news reports. Knowing this conversion helps you navigate everyday calculations with greater confidence.
-
Science and Engineering: The conversion between fractions and percentages is crucial in scientific and engineering fields, especially when dealing with measurements, ratios, and proportions. This conversion is fundamental in accurately interpreting experimental data and designing models.
Advanced Concepts and Further Exploration
Understanding the conversion of 1/50 to 2% forms the basis for tackling more complex percentage problems. Here are some areas for further exploration:
-
Converting Percentages to Fractions: Just as fractions can be converted to percentages, percentages can be converted back to fractions. This involves dividing the percentage by 100 and simplifying the resulting fraction.
-
Calculating Percentages of Larger Numbers: Applying the knowledge of 1/50 = 2% allows for efficient calculation of 2% of any number. For instance, 2% of 500 is simply (2/100) * 500 = 10.
-
Percentage Increase and Decrease: Understanding percentages allows for calculations of percentage increases and decreases, commonly used in finance, economics, and many other fields.
-
Compound Interest: This crucial financial concept heavily relies on the understanding of percentages and their application in repeated calculations.
Conclusion: Mastering Percentage Conversions
The ability to convert fractions to percentages is a valuable mathematical skill with broad implications. By understanding the various methods for converting 1/50 to 2%, you gain a foundation for tackling a wide range of percentage-related problems. This knowledge extends beyond simple conversions, facilitating deeper understanding of more complex concepts involving percentages and their practical applications in various fields. Remember that consistent practice and a solid understanding of fundamental principles are key to mastering percentage calculations. The more you work with these concepts, the more intuitive and easy they will become.
Latest Posts
Latest Posts
-
How Long Does It Take For A Fossil To Form
Apr 04, 2025
-
What Is A 2 Out Of 3
Apr 04, 2025
-
What Percent Is 10 Of 12
Apr 04, 2025
-
Write The Polynomial In Standard Form
Apr 04, 2025
-
Oz In A Cup Of Butter
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about What Is 1/50 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
