What Percent Is 10 Of 12
Kalali
Apr 04, 2025 · 5 min read
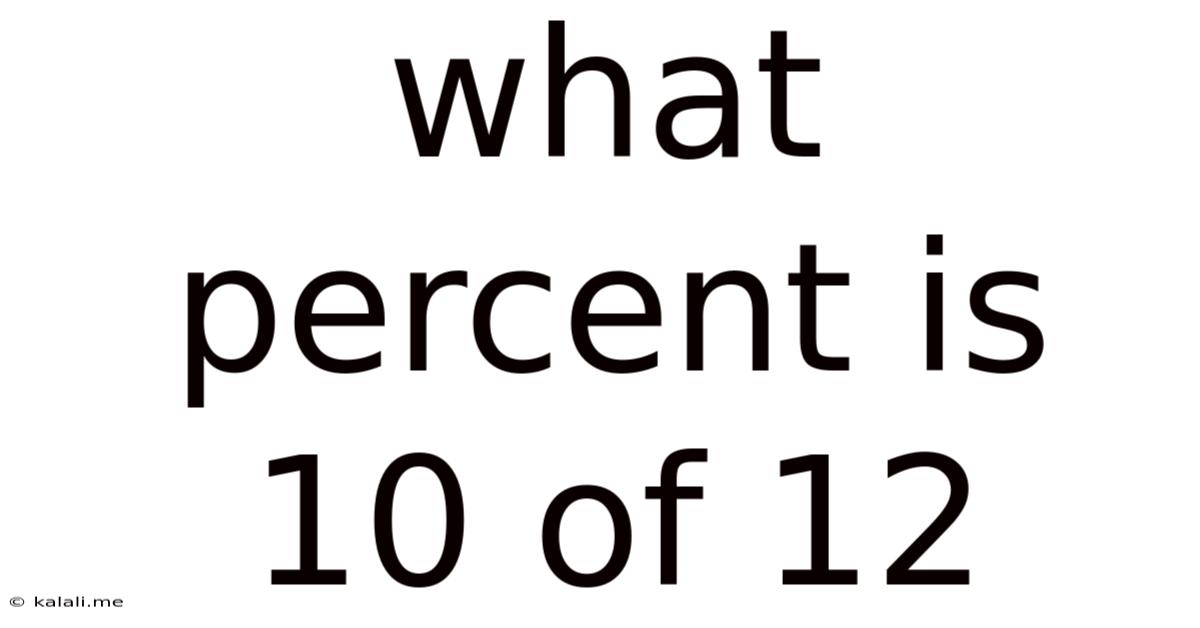
Table of Contents
What Percent is 10 of 12? A Deep Dive into Percentage Calculations
Finding out what percentage 10 represents of 12 might seem like a simple calculation, but understanding the underlying principles is crucial for a wide range of applications, from everyday budgeting and shopping to complex statistical analysis and scientific research. This article will not only answer the question directly but will also provide a comprehensive guide to understanding percentages, offering various methods of calculation and exploring practical applications.
Understanding Percentages: The Basics
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "per hundred," derived from the Latin "per centum." Therefore, 10% means 10 out of 100, or 10/100, which simplifies to 1/10. This fundamental concept forms the basis for all percentage calculations.
Calculating "What Percent is 10 of 12?" - Method 1: The Proportion Method
This method uses the concept of proportions, setting up an equation to solve for the unknown percentage.
-
Set up a proportion: We can represent the problem as a proportion:
x/100 = 10/12where 'x' represents the percentage we want to find. -
Cross-multiply: To solve for 'x', we cross-multiply:
12x = 1000 -
Solve for x: Divide both sides by 12:
x = 1000/12 = 83.333... -
Round to desired precision: We can round the result to a certain number of decimal places. Rounding to two decimal places, we get 83.33%. Therefore, 10 is approximately 83.33% of 12.
Calculating "What Percent is 10 of 12?" - Method 2: The Decimal Method
This method uses decimal representation to solve the problem.
-
Express the fraction: First, express the given numbers as a fraction: 10/12
-
Convert to a decimal: Divide the numerator (10) by the denominator (12): 10 ÷ 12 = 0.83333...
-
Convert to a percentage: Multiply the decimal by 100: 0.83333... × 100 = 83.333...%
-
Round to desired precision: Again, rounding to two decimal places, we get 83.33%.
Calculating "What Percent is 10 of 12?" - Method 3: Using a Calculator
Most calculators have a percentage function that simplifies the process.
-
Divide: Divide 10 by 12: 10 ÷ 12 = 0.83333...
-
Use the percentage function: Multiply the result by 100 using the percentage function (often represented by a '%' symbol) on your calculator. This will directly give you the percentage.
Practical Applications of Percentage Calculations
Understanding percentage calculations is essential in numerous real-world situations:
-
Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns all rely heavily on percentage calculations. For example, determining the interest earned on a savings account or the discount applied during a sale.
-
Retail: Pricing strategies, markups, and sale discounts are all based on percentages. Understanding these calculations allows consumers to make informed purchasing decisions and businesses to optimize pricing strategies.
-
Science: Percentage calculations are fundamental in scientific data analysis, expressing changes in experimental results or representing proportions in statistical studies. For example, calculating the percentage of a specific element in a compound or expressing the success rate of a treatment in a medical trial.
-
Everyday Life: Calculating tips at restaurants, determining the percentage of a task completed, or understanding the nutritional content of food (e.g., percentage of daily value) all involve percentage calculations.
Advanced Percentage Calculations: Beyond the Basics
While the problem "What percent is 10 of 12?" represents a straightforward calculation, many real-world applications require more advanced techniques. Let’s explore some of these:
-
Calculating Percentage Increase or Decrease: This involves determining the percentage change between two values. The formula is:
[(New Value - Old Value) / Old Value] × 100%. For instance, if a stock price rises from $10 to $12, the percentage increase is[(12 - 10) / 10] × 100% = 20%. -
Finding the Original Value: If you know the percentage and the final value after a percentage increase or decrease, you can work backward to find the original value. This often involves algebraic manipulation of the percentage change formula.
-
Compound Interest: This involves calculating interest on both the principal amount and accumulated interest. The formula for compound interest is:
A = P (1 + r/n)^(nt), where 'A' is the final amount, 'P' is the principal amount, 'r' is the annual interest rate, 'n' is the number of times interest is compounded per year, and 't' is the number of years. -
Statistical Analysis: Percentages are extensively used in statistics to represent proportions, frequencies, and probabilities. Confidence intervals, hypothesis testing, and various statistical measures rely on percentage calculations.
Addressing Common Percentage Calculation Mistakes
Several common mistakes can occur when working with percentages:
-
Incorrectly interpreting the problem: Ensure you clearly identify the base value (the "whole") before performing any calculations.
-
Mixing up percentages and decimal values: Remember to convert between decimal values and percentages accurately (multiplying by 100 to go from decimal to percentage and dividing by 100 to go from percentage to decimal).
-
Rounding errors: Rounding off intermediate results can lead to inaccuracies in the final answer. It's generally better to keep more decimal places during the calculation and round only the final result.
-
Inconsistent use of units: Always ensure consistent units are used throughout the calculation to avoid errors.
Conclusion:
Determining that 10 is approximately 83.33% of 12 is a seemingly simple calculation, but it underscores the fundamental importance of understanding percentages. From basic financial decisions to complex scientific analyses, proficiency in percentage calculations is an essential skill. By understanding the different methods, practical applications, and potential pitfalls outlined in this article, you can confidently tackle percentage problems and effectively apply this knowledge in diverse situations. Remember to practice regularly and apply your understanding to real-world problems to solidify your skills.
Latest Posts
Latest Posts
-
29 Out Of 35 In Perscen
Apr 10, 2025
-
How Many Centimeters Is 60 In
Apr 10, 2025
-
Least Common Multiple Of 7 And 6
Apr 10, 2025
-
What Is The Lowest Common Multiple Of 2 And 3
Apr 10, 2025
-
What Is 5 7 As A Percent
Apr 10, 2025
Related Post
Thank you for visiting our website which covers about What Percent Is 10 Of 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.