What Is 10 To The Power Of 5
Kalali
Apr 08, 2025 · 6 min read
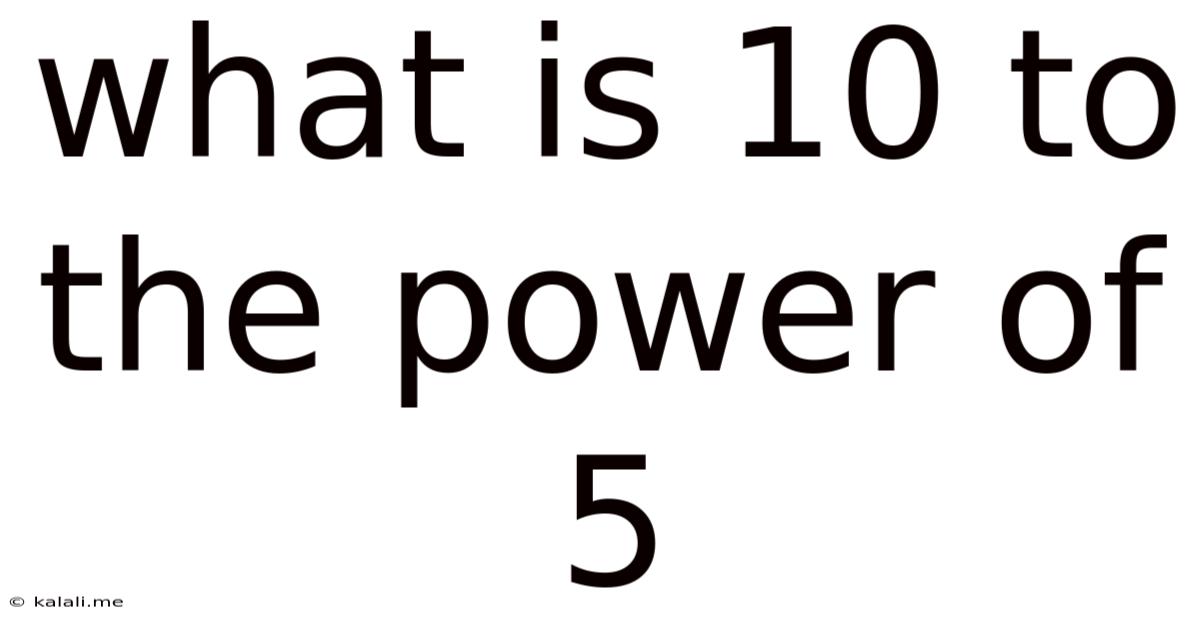
Table of Contents
What is 10 to the Power of 5? A Deep Dive into Exponentiation and its Applications
What is 10 to the power of 5? At first glance, this seems like a simple question with a straightforward answer. But delving deeper reveals a fascinating exploration of exponentiation, its practical applications in various fields, and its significance in understanding larger mathematical concepts. This article will not only answer the core question but also provide a comprehensive understanding of exponential notation, its uses in science, technology, and everyday life, and its connection to other mathematical ideas.
Meta Description: Discover the answer to "What is 10 to the power of 5?" This comprehensive guide explores exponentiation, its real-world applications in science, technology, and finance, and its connection to larger mathematical concepts. Learn about scientific notation, significant figures, and more!
The answer to "10 to the power of 5" is simply 100,000 (one hundred thousand). This is because exponentiation, represented by the superscript number (the exponent), indicates repeated multiplication. In this case, 10 to the power of 5 means 10 multiplied by itself five times: 10 x 10 x 10 x 10 x 10 = 100,000.
Understanding Exponentiation: Beyond the Basics
While calculating 10 to the power of 5 is relatively straightforward, understanding the broader concept of exponentiation is crucial for grasping its significance. Exponentiation is a fundamental mathematical operation where a base number is multiplied by itself a specified number of times, determined by the exponent. It's represented as b<sup>n</sup>, where 'b' is the base and 'n' is the exponent.
For instance:
- 2<sup>3</sup> = 2 x 2 x 2 = 8
- 5<sup>2</sup> = 5 x 5 = 25
- 10<sup>4</sup> = 10 x 10 x 10 x 10 = 10,000
The exponent indicates the number of times the base is used as a factor in the multiplication. When the exponent is 1, the result is simply the base itself (e.g., 10<sup>1</sup> = 10). When the exponent is 0, the result is always 1 (e.g., 10<sup>0</sup> = 1), except when the base is 0 (0<sup>0</sup> is undefined). Negative exponents represent reciprocals (e.g., 10<sup>-2</sup> = 1/10<sup>2</sup> = 1/100 = 0.01).
The Significance of 10 to the Power of 5
The number 100,000 (10<sup>5</sup>) holds particular significance due to its use in representing large quantities. It's frequently encountered in various contexts:
-
Finance: 100,000 represents a significant sum of money, often used in discussions about investments, loans, or business transactions. Understanding exponential growth is crucial in comprehending compound interest calculations, where initial investments grow exponentially over time.
-
Science: In scientific notation, 10<sup>5</sup> is used to express large numbers concisely. For instance, the speed of light in a vacuum is approximately 3 x 10<sup>8</sup> meters per second. Using powers of 10 simplifies the representation of extremely large or small values.
-
Technology: Data storage capacities are often expressed using powers of 10. A hard drive with a capacity of 100,000 megabytes could be expressed as 10<sup>5</sup> MB. Understanding exponential growth in computing power and data storage is crucial in evaluating technological advancements.
-
Everyday Life: While less frequent than in specialized fields, numbers of this magnitude can occur in population statistics, geographic measurements (e.g., the area of a large land mass), or even in lottery winnings.
Scientific Notation and Significant Figures
The concept of 10<sup>5</sup> is intrinsically linked to scientific notation, a standardized way to represent numbers, particularly very large or very small ones. Scientific notation expresses a number as a product of a coefficient and a power of 10. The coefficient is always a number between 1 and 10, while the power of 10 indicates the magnitude of the number.
For example:
- 3,500,000 can be written as 3.5 x 10<sup>6</sup>
- 0.000042 can be written as 4.2 x 10<sup>-5</sup>
Scientific notation simplifies calculations and comparisons of extremely large or small numbers. It's widely used in science, engineering, and computer science.
Closely related to scientific notation is the concept of significant figures, which refers to the number of digits in a value that carry meaning contributing to its measurement resolution. When dealing with large numbers like 100,000, the number of significant figures depends on the precision of the measurement. If the number is exactly 100,000, it has one significant figure. However, if it's a rounded number, it could have more significant figures depending on the original measurement's precision.
Expanding the Concept: Higher Powers of 10
Understanding 10<sup>5</sup> provides a foundation for understanding higher powers of 10. As the exponent increases, the magnitude of the number grows exponentially. Consider the following:
- 10<sup>6</sup> = 1,000,000 (one million)
- 10<sup>7</sup> = 10,000,000 (ten million)
- 10<sup>8</sup> = 100,000,000 (one hundred million)
- 10<sup>9</sup> = 1,000,000,000 (one billion)
These higher powers of 10 are frequently used to represent vast quantities in various scientific and technological fields. For instance, gigabytes (GB) in computer memory are expressed as 10<sup>9</sup> bytes.
Applications in Various Fields
The concept of exponentiation, particularly with a base of 10, has wide-ranging applications across various disciplines:
1. Physics and Engineering: Powers of 10 are fundamental to expressing large distances (light-years, astronomical units), small measurements (nanometers, angstroms), and vast energies (measured in joules or kilowatt-hours).
2. Chemistry: Molarity, a crucial concept in chemistry, uses powers of 10 to represent concentrations of solutions. The Avogadro constant (approximately 6.022 x 10<sup>23</sup>) describes the number of constituent particles in one mole of a substance.
3. Biology: Bacterial growth often follows an exponential pattern. Understanding exponential growth is crucial for predicting population sizes and controlling bacterial infections. Similarly, population dynamics in ecology are often modeled using exponential functions.
4. Economics and Finance: Compound interest, exponential growth of investments, and economic models often rely heavily on exponential functions and powers of 10 to simplify representations of large financial figures. Inflation and economic forecasts also use exponential functions for projection.
5. Computer Science: Binary numbers (base-2) are fundamental in computing. While not directly involving powers of 10, understanding exponentiation is essential for comprehending binary representations and data storage. The processing power of computers, measured in gigahertz (GHz), utilizes powers of 10.
Beyond Powers of 10: Other Bases
While this article focuses on powers of 10, it's important to note that exponentiation applies to any base number. Understanding the principles discussed here can be extended to other bases, such as:
-
Base 2 (Binary): Fundamental in computer science, binary numbers use only 0 and 1. Powers of 2 are used to represent values in computer memory and processing.
-
Base 8 (Octal): Sometimes used in computer programming.
-
Base 16 (Hexadecimal): Commonly used in computer programming and color codes.
Mastering exponentiation with base 10 provides a solid foundation for understanding and applying this crucial mathematical concept across various fields.
Conclusion: The Expanding World of Exponentiation
This in-depth exploration of "What is 10 to the power of 5?" reveals that the answer, 100,000, is just the beginning. The underlying concept of exponentiation is fundamental to numerous fields, providing a powerful tool for representing and working with extremely large or small numbers. From scientific notation and significant figures to applications in finance, technology, and various scientific disciplines, understanding exponentiation is essential for navigating a world increasingly reliant on precise numerical representation and exponential growth models. The seemingly simple question "What is 10 to the power of 5?" opens a door to a much wider understanding of mathematical principles and their impact on the world around us.
Latest Posts
Latest Posts
-
2 Km Is How Many Meters
Apr 17, 2025
-
What Is The Fraction Of 1 6
Apr 17, 2025
-
What Percentage Of 16 Is 10
Apr 17, 2025
-
16 Out Of 23 As A Percentage
Apr 17, 2025
-
How To Get Cube Root On Calculator
Apr 17, 2025
Related Post
Thank you for visiting our website which covers about What Is 10 To The Power Of 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.