What Is 15 Percent Of 15
Kalali
Apr 24, 2025 · 5 min read
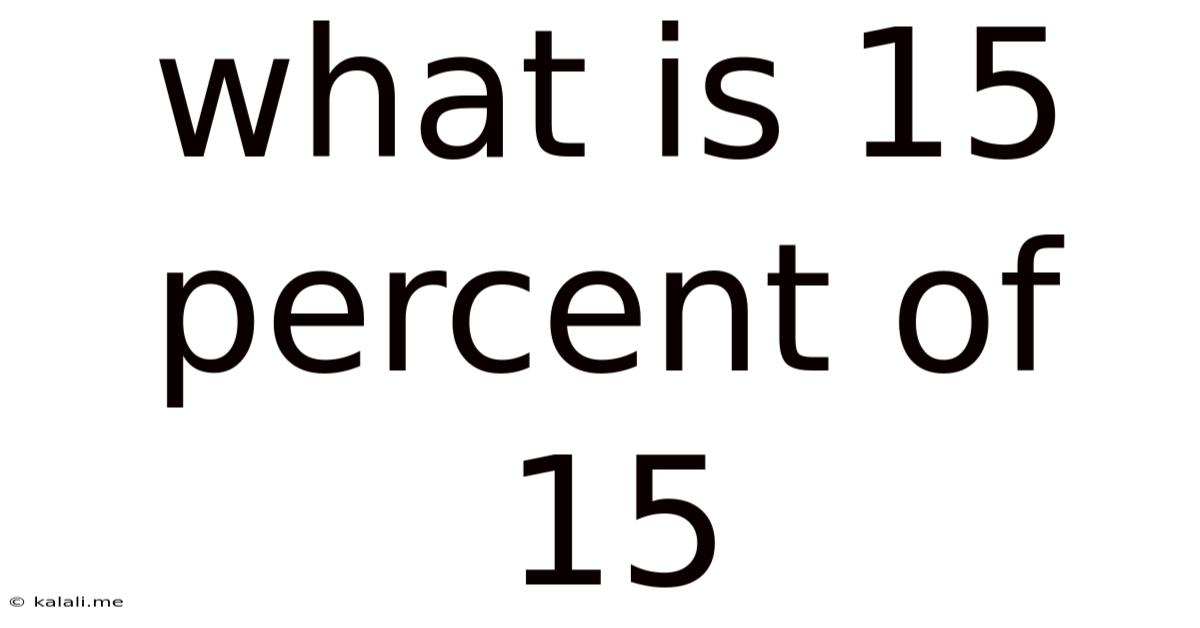
Table of Contents
What is 15 Percent of 15? A Deep Dive into Percentage Calculations and Their Applications
What is 15 percent of 15? The answer, as a simple calculation reveals, is 2.25. But this seemingly straightforward question opens a door to a world of practical applications and mathematical concepts far beyond basic arithmetic. This article will not only solve the problem but will explore the broader implications of percentage calculations, their use in everyday life, and delve into the mathematical principles behind them. We'll also look at different methods for calculating percentages and how these calculations are crucial in various fields. This comprehensive guide will equip you with a solid understanding of percentages, empowering you to confidently tackle similar problems and appreciate their significance in the real world.
Understanding Percentages: A Foundation for Calculation
Before diving into the specifics of calculating 15% of 15, let's establish a firm understanding of what percentages represent. A percentage is simply a fraction expressed as a part of 100. The symbol "%" signifies "per hundred" or "out of 100." Therefore, 15% can be written as 15/100 or 0.15 in decimal form. This understanding forms the basis of all percentage calculations. Understanding this fundamental concept is crucial for comprehending the various methods used to compute percentages.
Calculating 15% of 15: Three Different Approaches
There are several ways to calculate 15% of 15. Let's explore three common methods:
1. The Decimal Method:
This is arguably the most straightforward approach. We convert the percentage to its decimal equivalent (15% = 0.15) and then multiply it by the number we're finding the percentage of:
15% of 15 = 0.15 * 15 = 2.25
This method is efficient and easily adaptable to various percentage calculations. Its simplicity makes it ideal for quick calculations, especially when using a calculator.
2. The Fraction Method:
This method uses the fraction representation of the percentage. We express 15% as 15/100 and then multiply it by 15:
15% of 15 = (15/100) * 15 = 225/100 = 2.25
This method offers a deeper understanding of the underlying mathematical principles. It's particularly helpful in situations where simplification of fractions is possible, potentially leading to easier calculations.
3. The Proportion Method:
This method uses the concept of proportions to solve the problem. We set up a proportion:
15/100 = x/15
Where 'x' represents the value we're trying to find (15% of 15). To solve for 'x', we cross-multiply:
100x = 15 * 15 100x = 225 x = 225/100 = 2.25
This method is useful for understanding the relationship between the percentage, the whole, and the part. It demonstrates the proportional relationship and is a valuable tool in various mathematical problems.
Real-World Applications of Percentage Calculations
Percentage calculations are ubiquitous in everyday life. Understanding them is essential for navigating various financial, scientific, and everyday situations. Here are just a few examples:
-
Sales and Discounts: Retail stores frequently advertise discounts as percentages. Calculating the final price after a discount involves a percentage calculation. For example, a 20% discount on a $50 item means a saving of $10 (20% of $50), resulting in a final price of $40.
-
Taxes: Sales taxes and income taxes are usually expressed as percentages. Calculating the total cost of an item including sales tax requires a percentage calculation. Similarly, determining the amount of income tax payable involves percentage calculations based on tax brackets.
-
Tips and Gratuities: Calculating tips in restaurants usually involves determining a percentage of the total bill. A 15% tip on a $75 meal, for instance, would be $11.25 (15% of $75).
-
Interest Rates: Interest rates on loans, savings accounts, and investments are expressed as percentages. Understanding percentage calculations is vital for comparing different interest rates and making informed financial decisions.
-
Statistics and Data Analysis: Percentages are frequently used to represent proportions within datasets. For example, survey results are often expressed as percentages to illustrate the proportion of respondents who selected a particular answer. Understanding these percentages is crucial for interpreting data and drawing meaningful conclusions.
-
Profit Margins and Markups: Businesses use percentages to determine profit margins and markups. The profit margin is the percentage of revenue remaining after deducting all costs. Markup is the percentage increase over the cost price to determine the selling price.
-
Scientific Measurements and Experiments: Percentages are often used in scientific studies to represent changes in variables, error margins, or concentrations. For example, expressing the percentage change in a population over a certain period or describing the concentration of a chemical solution.
Beyond the Basics: Advanced Percentage Calculations
While calculating 15% of 15 is a simple problem, the concept of percentages extends to more complex scenarios. Some advanced applications include:
-
Compound Interest: This involves calculating interest not just on the principal amount but also on the accumulated interest. Understanding compound interest is critical for long-term financial planning and investments.
-
Percentage Change: Calculating the percentage increase or decrease between two values. This is useful for analyzing trends and comparing data over time. For example, analyzing the percentage growth of a company’s revenue year over year.
-
Percentage Points: Understanding the difference between percentage change and percentage points is vital for accurate interpretation. A change from 10% to 20% is a 100% increase, but it's also a 10 percentage point increase.
-
Weighted Averages: Calculating the average of a set of values, where each value has a different weight or importance. This is commonly used in academic grading systems or financial portfolio analysis.
Conclusion: The Significance of Understanding Percentages
The seemingly simple question, "What is 15 percent of 15?" serves as a gateway to a much broader understanding of percentages and their crucial role in numerous aspects of life. From everyday transactions to complex financial models, the ability to accurately calculate and interpret percentages is an invaluable skill. Mastering this fundamental concept empowers individuals to make informed decisions, analyze data effectively, and confidently navigate a world filled with numerical representations. This comprehensive exploration has not only provided the answer (2.25) but has also illuminated the profound applications and underlying mathematical principles of percentage calculations, solidifying their importance in a diverse range of fields. The ability to perform these calculations accurately is essential for personal finance, business decisions, and a deeper understanding of the world around us.
Latest Posts
Latest Posts
-
Which Is An Interconnection Of Food Chains In An Ecosystem
Apr 24, 2025
-
5 Is What Percent Of 9
Apr 24, 2025
-
Cuanto Es 1 M En Pies
Apr 24, 2025
-
How Many Ml Is 26 Ounces
Apr 24, 2025
-
How Are The Building Blocks Of Organic Molecules Like Bricks
Apr 24, 2025
Related Post
Thank you for visiting our website which covers about What Is 15 Percent Of 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.