What Is 18/24 As A Percent
Kalali
Apr 09, 2025 · 5 min read
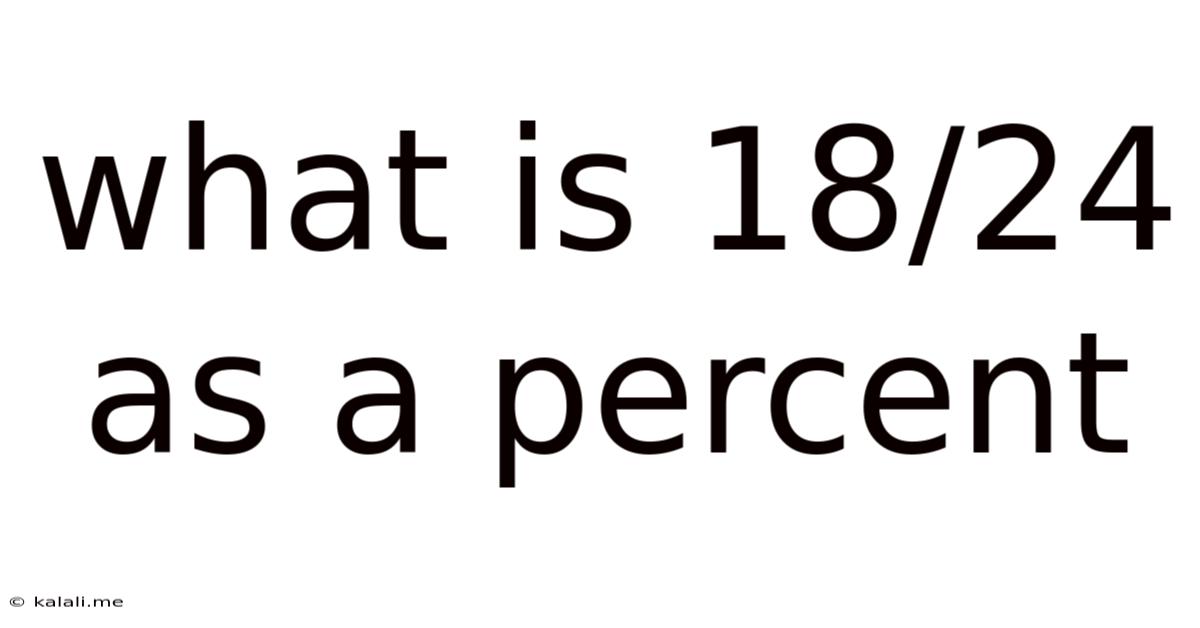
Table of Contents
What is 18/24 as a Percent? A Comprehensive Guide to Fraction-to-Percentage Conversion
This article will comprehensively explain how to convert the fraction 18/24 into a percentage, exploring the underlying principles of fraction-to-percentage conversion and providing multiple methods for solving similar problems. We'll also delve into the practical applications of understanding these conversions and touch upon related mathematical concepts. Understanding this simple conversion is crucial for various fields, from basic math and finance to data analysis and more.
Meta Description: Learn how to convert the fraction 18/24 into a percentage. This guide provides multiple methods, explains the underlying principles, and explores practical applications of fraction-to-percentage conversions.
Understanding Fractions and Percentages
Before diving into the specific conversion of 18/24, let's refresh our understanding of fractions and percentages.
A fraction represents a part of a whole. It's expressed as a ratio of two numbers, the numerator (top number) and the denominator (bottom number). In our case, 18/24 signifies 18 parts out of a total of 24 parts.
A percentage is a way of expressing a number as a fraction of 100. It represents a proportion per hundred. The symbol "%" is used to denote percentages. For instance, 50% means 50 out of 100, or 50/100.
Method 1: Simplifying the Fraction First
The most straightforward approach involves simplifying the fraction before converting it to a percentage. This simplifies the calculations and often leads to a cleaner result.
-
Find the Greatest Common Divisor (GCD): The GCD of 18 and 24 is 6. This means both numbers are divisible by 6.
-
Simplify the Fraction: Divide both the numerator and the denominator by the GCD:
18 ÷ 6 = 3 24 ÷ 6 = 4
This simplifies the fraction 18/24 to 3/4.
-
Convert the Simplified Fraction to a Decimal: Divide the numerator by the denominator:
3 ÷ 4 = 0.75
-
Convert the Decimal to a Percentage: Multiply the decimal by 100 and add the percentage symbol:
0.75 × 100 = 75%
Therefore, 18/24 is equal to 75%.
Method 2: Direct Conversion from Fraction to Percentage
This method involves a direct conversion without simplifying the fraction beforehand. While it might seem slightly more complex initially, it's equally valid and can be useful in certain situations.
-
Convert the Fraction to a Decimal: Divide the numerator by the denominator:
18 ÷ 24 = 0.75
-
Convert the Decimal to a Percentage: Multiply the decimal by 100 and add the percentage symbol:
0.75 × 100 = 75%
As you can see, even without simplifying the fraction first, we arrive at the same result: 75%.
Method 3: Using Proportions
This method employs the concept of proportions to solve the problem. We set up a proportion to find the equivalent percentage.
-
Set up a Proportion: We want to find x, where x/100 = 18/24.
-
Cross-Multiply: This gives us 24x = 1800.
-
Solve for x: Divide both sides by 24:
x = 1800 ÷ 24 = 75
Therefore, x = 75%, confirming that 18/24 is equal to 75%.
Practical Applications of Fraction-to-Percentage Conversions
The ability to convert fractions to percentages is crucial in numerous real-world scenarios:
-
Finance: Calculating interest rates, discounts, profit margins, and tax rates often involves converting fractions to percentages. For example, if a store offers a 1/4 discount, you need to convert this fraction to a percentage (25%) to determine the actual discount amount.
-
Data Analysis: Representing data in percentages makes it easier to understand and compare different proportions. For example, if a survey shows 18 out of 24 respondents prefer a certain product, converting this to 75% provides a clear and concise representation of preference.
-
Probability: Probability is often expressed as a fraction, but converting it to a percentage provides a more intuitive understanding of the likelihood of an event occurring.
-
Everyday Life: Calculating tips, splitting bills, or understanding sale prices frequently requires converting fractions to percentages.
Understanding Percentage Increase and Decrease
While this article focuses on converting a single fraction, it's important to understand related concepts like percentage increase and decrease. These concepts build upon the foundation of fraction-to-percentage conversions.
A percentage increase represents the relative increase in a value compared to its original value. For instance, if a value increases from 20 to 25, the percentage increase is calculated as follows:
- Find the difference: 25 - 20 = 5
- Divide the difference by the original value: 5 ÷ 20 = 0.25
- Convert to percentage: 0.25 × 100 = 25%
Therefore, there is a 25% increase.
A percentage decrease works similarly, but the difference is subtracted from the original value. For example, if a value decreases from 50 to 40:
- Find the difference: 50 - 40 = 10
- Divide the difference by the original value: 10 ÷ 50 = 0.2
- Convert to percentage: 0.2 × 100 = 20%
Therefore, there is a 20% decrease.
Further Exploration: Working with More Complex Fractions
The principles discussed in this article apply to all fraction-to-percentage conversions. Even more complex fractions, those with larger numerators and denominators or those involving decimals, can be converted using the same methods. The key is to always follow the steps systematically: simplify the fraction if possible, convert to a decimal, and then convert the decimal to a percentage.
Remember to always double-check your calculations and ensure your final answer makes sense within the context of the problem.
Conclusion
Converting fractions to percentages is a fundamental skill with broad applicability. Understanding the various methods – simplifying the fraction, direct decimal conversion, and using proportions – equips you with multiple tools to tackle these conversions efficiently. This understanding extends beyond simple conversions to encompass broader mathematical concepts, like calculating percentage increases and decreases, which are essential for various applications in daily life, finance, and data analysis. Mastering this skill will enhance your problem-solving abilities and improve your understanding of numerical representation.
Latest Posts
Latest Posts
-
What Percentage Of 6 Is 30
Apr 17, 2025
-
Flowering Plants Separated Into Different Classifications
Apr 17, 2025
-
How Much Is 33 Inches In Feet
Apr 17, 2025
-
What Is 205 Celsius In Fahrenheit
Apr 17, 2025
-
71 Inches Is How Many Cm
Apr 17, 2025
Related Post
Thank you for visiting our website which covers about What Is 18/24 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.