What Percentage Of 6 Is 30
Kalali
Apr 17, 2025 · 5 min read
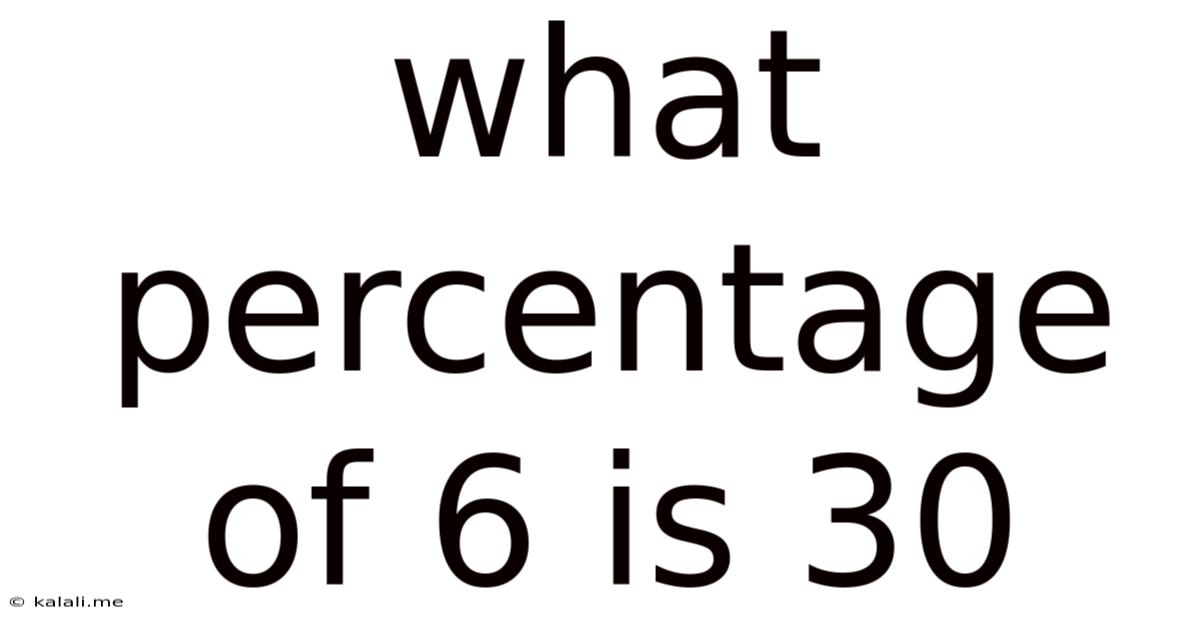
Table of Contents
What Percentage of 6 is 30? Understanding Percentage Calculations
This seemingly simple question, "What percentage of 6 is 30?", unveils a fundamental concept in mathematics: percentages. While the answer might seem counterintuitive at first glance, understanding the underlying process is crucial for various applications in everyday life, from calculating discounts and taxes to interpreting statistics and analyzing financial data. This article delves deep into solving this problem, exploring the different methods, explaining the logic behind percentage calculations, and demonstrating how to apply these techniques to similar problems. We'll also explore the broader context of percentages and their importance in various fields.
Understanding Percentages: A Foundation
A percentage is simply a fraction expressed as a part of 100. The term "percent" originates from the Latin "per centum," meaning "out of a hundred." Therefore, 50% means 50 out of 100, or 50/100, which simplifies to 1/2 or 0.5. This fundamental understanding allows us to translate percentages into decimals and fractions, and vice versa. This flexibility is key to solving percentage problems efficiently.
Method 1: Using the Proportion Method
This method is arguably the most straightforward approach to solving "What percentage of 6 is 30?". We set up a proportion, equating two ratios:
- Ratio 1: The part (30) to the whole (6)
- Ratio 2: The percentage (x) to 100
This leads to the following equation:
30/6 = x/100
To solve for x, we cross-multiply:
30 * 100 = 6 * x
3000 = 6x
x = 3000 / 6
x = 500
Therefore, 30 is 500% of 6.
Method 2: Using the Decimal Method
This method involves converting the percentage to a decimal and then using it to solve the problem. We start by setting up the equation:
6 * x = 30
To isolate x, we divide both sides by 6:
x = 30 / 6
x = 5
This represents the decimal equivalent of the percentage. To convert this decimal to a percentage, we multiply by 100:
5 * 100 = 500%
Again, we arrive at the answer: 30 is 500% of 6.
Why 500%? Interpreting the Result
The result of 500% might seem surprising at first. We're used to percentages being between 0% and 100%, representing a portion of a whole. However, percentages greater than 100% simply indicate that the "part" is larger than the "whole." In this case, 30 is more than 6, hence the percentage exceeds 100%. This highlights the flexibility of percentages in representing various relationships between numbers, not just fractions of a whole.
Practical Applications of Percentage Calculations
Understanding percentage calculations is essential in numerous real-world situations:
- Finance: Calculating interest rates, loan repayments, profit margins, investment returns, and tax deductions.
- Retail: Determining discounts, sale prices, and value-added tax (VAT).
- Statistics: Analyzing data, interpreting survey results, and understanding population trends.
- Science: Expressing experimental results, calculating concentrations, and analyzing statistical significance.
- Everyday Life: Tip calculations, comparing prices, and understanding proportions in recipes.
Solving Similar Problems: A Step-by-Step Guide
Let's apply the methods learned to a few similar problems:
Problem 1: What percentage of 15 is 45?
- Proportion Method: 45/15 = x/100 => x = 300%
- Decimal Method: 15 * x = 45 => x = 3 => 3 * 100 = 300%
Problem 2: What percentage of 20 is 5?
- Proportion Method: 5/20 = x/100 => x = 25%
- Decimal Method: 20 * x = 5 => x = 0.25 => 0.25 * 100 = 25%
Problem 3: What percentage of 8 is 12?
- Proportion Method: 12/8 = x/100 => x = 150%
- Decimal Method: 8 * x = 12 => x = 1.5 => 1.5 * 100 = 150%
Advanced Percentage Calculations: Beyond the Basics
While the problems above are relatively straightforward, percentage calculations can become more complex. Consider scenarios involving multiple percentages, percentage increases or decreases, and compound interest. These advanced calculations often require a deeper understanding of algebraic principles and may involve multiple steps. However, the fundamental concepts remain the same: translating percentages into decimals and fractions, and employing logical reasoning to solve for the unknown variable.
Percentage Increase and Decrease
Calculating percentage increases and decreases is a common application in various fields. For instance, determining the percentage change in sales figures, population growth, or investment values. The formula for percentage increase is:
[(New Value - Old Value) / Old Value] * 100
And for percentage decrease:
[(Old Value - New Value) / Old Value] * 100
Compound Interest
Compound interest involves earning interest on both the principal amount and accumulated interest. This concept is crucial in financial planning and investment strategies. The formula for compound interest is:
A = P (1 + r/n)^(nt)
Where:
- A = the future value of the investment/loan, including interest
- P = the principal investment amount (the initial deposit or loan amount)
- r = the annual interest rate (decimal)
- n = the number of times that interest is compounded per year
- t = the number of years the money is invested or borrowed for
Conclusion: Mastering Percentages for Success
Understanding percentages is a foundational skill applicable across numerous disciplines. This article has explored the core concepts of percentage calculations, presented multiple methods for solving percentage problems, and illustrated the practical applications in diverse contexts. From simple calculations to advanced scenarios involving compound interest and percentage changes, mastering percentages equips individuals with valuable tools for navigating the complexities of the modern world. By understanding the underlying principles and practicing different solution methods, you can confidently tackle any percentage-related challenge and effectively interpret data in various professional and personal situations. Remember that practice is key; the more you work with percentages, the more intuitive and effortless these calculations will become.
Latest Posts
Latest Posts
-
How Many Pounds In 2000 Grams
Apr 19, 2025
-
What Percent Is 14 Out Of 20
Apr 19, 2025
-
What Is 3 Percent Of 10000
Apr 19, 2025
-
4 Liters Is How Many Milliliters
Apr 19, 2025
-
Cuanto Es 30 Grados Centigrados En Fahrenheit
Apr 19, 2025
Related Post
Thank you for visiting our website which covers about What Percentage Of 6 Is 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.