What Is 2/3 Cup + 2/3 Cup
Kalali
Apr 17, 2025 · 5 min read
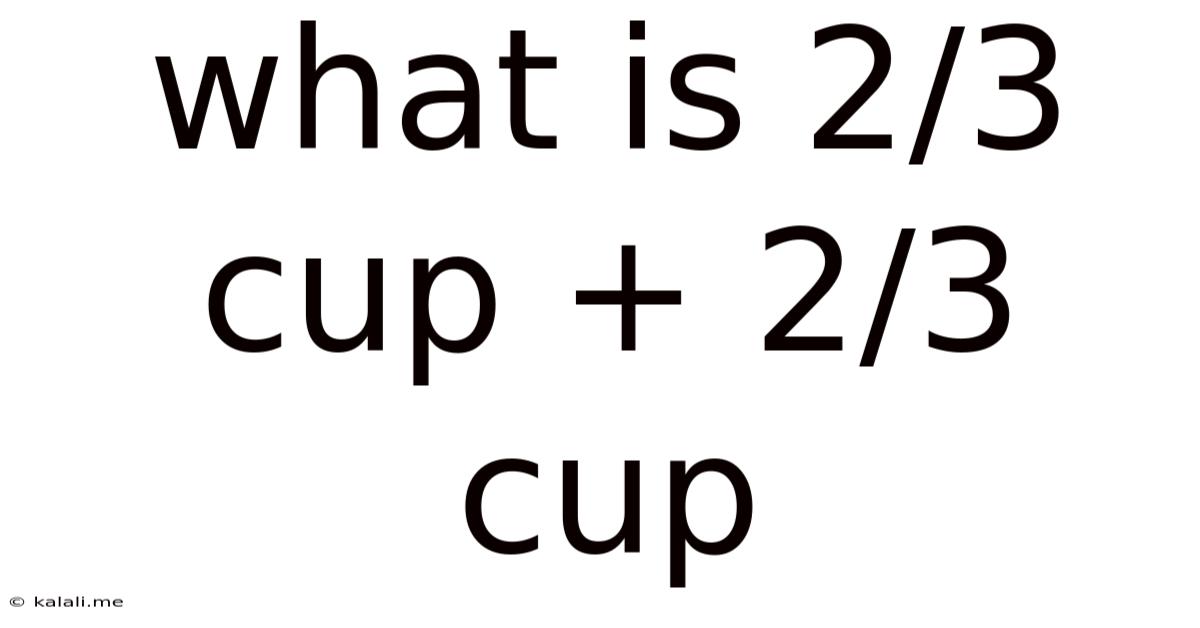
Table of Contents
What is 2/3 Cup + 2/3 Cup? A Deep Dive into Fraction Addition and Culinary Applications
This seemingly simple question, "What is 2/3 cup + 2/3 cup?", opens the door to a fascinating exploration of fractions, their practical applications in everyday life, particularly in cooking and baking, and the importance of precise measurements in culinary arts. While the answer itself is straightforward, understanding the underlying mathematical principles and their real-world implications enhances our understanding of both mathematics and cooking. This article will delve into the solution, explore different methods for solving the problem, and discuss the significance of accurate measurements in recipes.
Meta Description: Learn how to easily add fractions, specifically 2/3 cup + 2/3 cup, and understand the importance of precise measurements in cooking and baking. This guide provides multiple methods for solving the problem and discusses real-world applications.
Understanding Fractions: A Quick Refresher
Before we tackle the problem, let's briefly review the fundamentals of fractions. A fraction represents a part of a whole. It consists of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into. In our case, we're dealing with the fraction 2/3, where 2 is the numerator and 3 is the denominator. This means we have 2 out of 3 equal parts of a whole cup.
Solving 2/3 Cup + 2/3 Cup: The Simple Approach
Adding fractions with the same denominator is remarkably straightforward. Since both fractions in our problem (2/3 cup + 2/3 cup) have the same denominator (3), we simply add the numerators and keep the denominator the same:
2/3 + 2/3 = (2 + 2) / 3 = 4/3
This means that 2/3 cup + 2/3 cup equals 4/3 cups.
Converting Improper Fractions to Mixed Numbers
The result, 4/3, is an improper fraction because the numerator (4) is larger than the denominator (3). In culinary contexts, improper fractions are less intuitive than mixed numbers. A mixed number combines a whole number and a proper fraction. To convert 4/3 to a mixed number, we divide the numerator (4) by the denominator (3):
4 ÷ 3 = 1 with a remainder of 1
This means that 4/3 is equivalent to 1 and 1/3. Therefore, 2/3 cup + 2/3 cup = 1 and 1/3 cups, or 1 1/3 cups. This is a much more practical way to express the quantity in a recipe.
Visualizing the Addition: A Practical Example
Imagine you have two measuring cups. You fill one to the 2/3 cup mark and another to the same level. Visually, you can see that you have a little more than one full cup. By combining the contents of both cups, you'll have one full cup and a third of a cup remaining, confirming our calculation of 1 1/3 cups. This visual representation helps solidify the mathematical concept.
Different Methods for Adding Fractions: A Deeper Dive
While the direct addition method works well for fractions with a common denominator, let's explore other approaches to strengthen our understanding of fraction arithmetic:
-
Using a visual aid: Draw a circle and divide it into three equal sections. Shade two sections to represent 2/3. Do this for another circle. Combining both circles' shaded sections demonstrates that you have four out of three sections shaded, again illustrating 4/3 or 1 1/3.
-
Converting to decimals: Fractions can be converted to decimals by dividing the numerator by the denominator. 2/3 is approximately 0.667. Adding 0.667 + 0.667 equals 1.334, which is close to 1 1/3. This method is less precise but provides an alternative approach.
-
Finding a common denominator (for fractions with different denominators): While not applicable to our specific problem, this method is crucial for adding fractions with unlike denominators. You find the least common multiple (LCM) of the denominators and then convert each fraction to an equivalent fraction with the common denominator before adding the numerators.
The Importance of Accurate Measurements in Cooking and Baking
The seemingly small difference between 2/3 cup and 1 1/3 cups can have significant consequences in cooking and baking. Recipes are meticulously designed with specific ratios of ingredients. Inaccurate measurements can lead to:
-
Inadequate rising in baked goods: Too little liquid can result in a dense, dry cake or bread, while too much can lead to a flat, gummy texture.
-
Altered flavors and textures: Incorrect proportions can drastically alter the overall taste and consistency of a dish, potentially ruining the intended outcome.
-
Inconsistent results: Using imprecise measurements makes it difficult to reproduce successful results consistently.
-
Safety concerns (in some cases): In certain recipes, accurate measurements are crucial for food safety. For example, incorrect ratios of ingredients in preserving may lead to spoilage.
Beyond the Cup: Applying Fraction Addition to Other Measurements
The principles of fraction addition apply to various culinary measurements beyond cups, including tablespoons, teaspoons, ounces, and grams. Mastering fraction arithmetic is essential for accurately following recipes and adapting them to different needs. For example, if a recipe calls for 1/4 cup of butter and you want to double the recipe, you'll need to calculate 1/4 cup + 1/4 cup = 1/2 cup of butter. This applies to scaling recipes up or down.
Conclusion: Mastering Fractions for Culinary Success
While adding 2/3 cup + 2/3 cup might seem trivial at first glance, it highlights the importance of understanding fundamental mathematical concepts and their practical applications in everyday life. Precise measurements are vital for successful cooking and baking, ensuring consistent and delicious results. Mastering fraction arithmetic isn't just about solving mathematical problems; it's about creating culinary masterpieces. By understanding the underlying principles and practicing different methods of solving fraction problems, you can improve your culinary skills and gain confidence in the kitchen. Remember, accurate measurement is the key to consistent and delicious results, whether you are baking a cake or preparing a savory dish. The seemingly simple act of adding fractions translates to a world of culinary possibilities.
Latest Posts
Latest Posts
-
How Much Is 160 Celsius In Fahrenheit
Apr 19, 2025
-
How Many Pounds In 2000 Grams
Apr 19, 2025
-
What Percent Is 14 Out Of 20
Apr 19, 2025
-
What Is 3 Percent Of 10000
Apr 19, 2025
-
4 Liters Is How Many Milliliters
Apr 19, 2025
Related Post
Thank you for visiting our website which covers about What Is 2/3 Cup + 2/3 Cup . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.