What Is 2/5 As A Percent
Kalali
Mar 14, 2025 · 5 min read
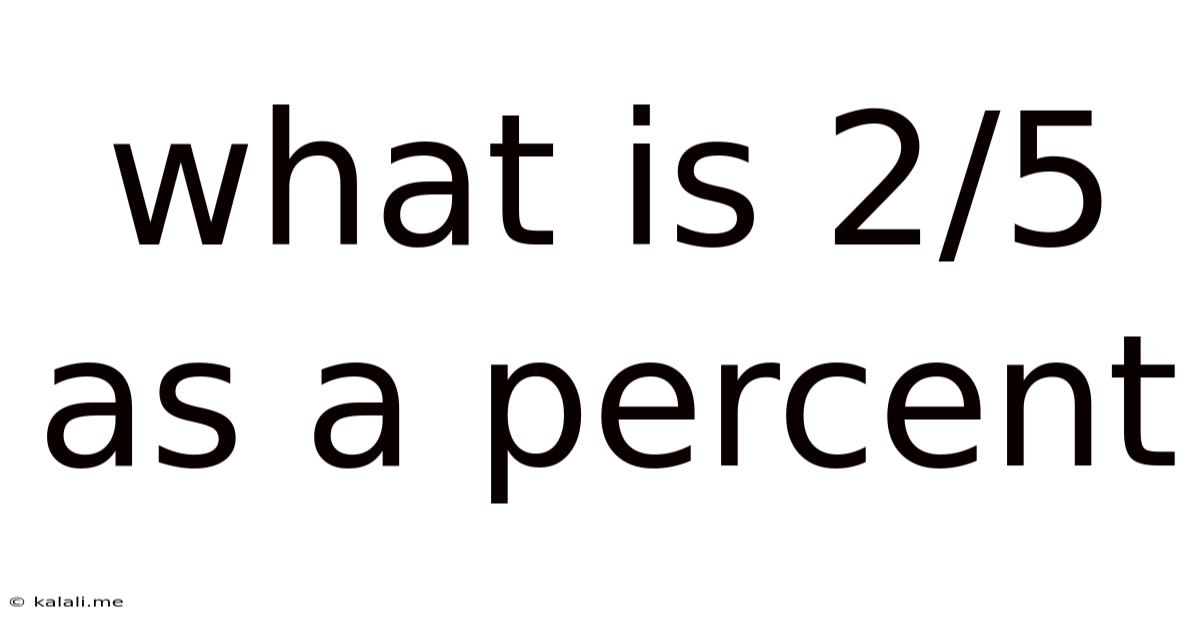
Table of Contents
What is 2/5 as a Percent? A Comprehensive Guide
Converting fractions to percentages is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts in shops to understanding statistical data. This comprehensive guide will delve into the process of converting the fraction 2/5 into a percentage, explaining the underlying principles and providing multiple approaches to solve this problem. We'll also explore the broader context of fraction-to-percentage conversions and their significance.
Understanding Fractions and Percentages
Before we tackle the conversion of 2/5 to a percentage, let's briefly review the concepts of fractions and percentages.
Fractions: A fraction represents a part of a whole. It consists of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates the number of parts we have, while the denominator indicates the total number of equal parts the whole is divided into. For example, in the fraction 2/5, 2 is the numerator and 5 is the denominator. This means we have 2 parts out of a total of 5 equal parts.
Percentages: A percentage is a way of expressing a number as a fraction of 100. The symbol "%" represents "per cent," meaning "out of one hundred." For instance, 50% means 50 out of 100, which is equivalent to the fraction 50/100, or 1/2. Percentages are used extensively to represent proportions, rates, and changes.
Method 1: Converting the Fraction Directly
The most straightforward method to convert 2/5 to a percentage involves two simple steps:
Step 1: Convert the fraction to a decimal. To do this, divide the numerator (2) by the denominator (5):
2 ÷ 5 = 0.4
Step 2: Convert the decimal to a percentage. Multiply the decimal by 100 and add the "%" symbol:
0.4 x 100 = 40%
Therefore, 2/5 is equal to 40%.
Method 2: Finding an Equivalent Fraction with a Denominator of 100
Another approach involves finding an equivalent fraction where the denominator is 100. This method highlights the relationship between fractions and percentages more directly.
To make the denominator 100, we need to multiply both the numerator and the denominator of 2/5 by the same number. Since 5 multiplied by 20 equals 100, we'll multiply both the numerator and the denominator by 20:
(2 x 20) / (5 x 20) = 40/100
Since a percentage is a fraction out of 100, 40/100 directly translates to 40%.
Method 3: Using Proportions
This method uses the concept of proportions to solve the problem. We can set up a proportion to find the percentage:
2/5 = x/100
To solve for x (the percentage), we cross-multiply:
5x = 200
Now, divide both sides by 5:
x = 40
Therefore, x = 40%, confirming that 2/5 is equal to 40%.
Real-World Applications of Percentage Conversions
Understanding how to convert fractions to percentages is crucial in various real-world scenarios:
-
Retail Discounts: Sales often advertise discounts as percentages (e.g., "40% off"). Knowing how to convert fractions to percentages helps you quickly calculate the actual savings. For example, if an item is marked down by 2/5, you know it's a 40% discount.
-
Financial Calculations: Interest rates, tax rates, and investment returns are frequently expressed as percentages. Converting fractions to percentages allows for easy comparison and analysis of financial data.
-
Statistical Analysis: In statistics, data is often represented as fractions or proportions. Converting these to percentages makes the data more understandable and easier to visualize using charts and graphs.
-
Scientific Measurements: In scientific fields, measurements are sometimes expressed as fractions. Converting these fractions to percentages provides a standardized and readily comparable format.
Beyond 2/5: Mastering Fraction-to-Percentage Conversions
The methods described above can be applied to convert any fraction to a percentage. Here's a general approach:
-
Divide the numerator by the denominator: This converts the fraction to a decimal.
-
Multiply the decimal by 100: This converts the decimal to a percentage. Remember to add the "%" symbol.
For example, let's convert 3/4 to a percentage:
-
3 ÷ 4 = 0.75
-
0.75 x 100 = 75%
Therefore, 3/4 is equal to 75%.
Dealing with Improper Fractions and Mixed Numbers
The methods described above primarily focus on proper fractions (where the numerator is smaller than the denominator). However, we can also apply these techniques to improper fractions (where the numerator is larger than the denominator) and mixed numbers (which combine a whole number and a fraction).
Improper Fractions: Convert the improper fraction to a mixed number first, then convert the fractional part to a percentage using the methods outlined previously. Finally, add the whole number to the percentage. For instance: 7/5 = 1 2/5 = 1 + 40% = 140%
Mixed Numbers: Separate the whole number and the fractional part. Convert the fractional part to a percentage and add it to the whole number. For example: 1 1/4 = 1 + 25% = 125%
Practice Makes Perfect
The key to mastering fraction-to-percentage conversions is practice. Try converting various fractions to percentages using the different methods described. This will help you develop a strong understanding of the concepts and build your mathematical skills.
Conclusion: The Significance of 40% (and other Percentages)
Understanding that 2/5 equals 40% allows for easier comprehension and application of proportional reasoning in numerous contexts. This knowledge forms a crucial building block for more advanced mathematical concepts and problem-solving in various fields. The ability to seamlessly convert between fractions and percentages demonstrates a fundamental understanding of numerical representation and proportional relationships. By practicing these conversions, you equip yourself with a valuable skill applicable across a wide spectrum of academic and professional endeavors. Mastering this simple yet essential conversion strengthens your mathematical fluency and enhances your ability to interpret and utilize numerical data effectively.
Latest Posts
Latest Posts
-
What Is Half Of 1 1 2
Jul 03, 2025
-
How Much Do A Sandwich Bag Weigh
Jul 03, 2025
-
Why Did The Obtuse Angle Go To The Beach
Jul 03, 2025
-
How Much Is Three Quarts Of Water
Jul 03, 2025
-
How Tall Is A 3 Story Building
Jul 03, 2025
Related Post
Thank you for visiting our website which covers about What Is 2/5 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.