What Is 2.6 In A Fraction
Kalali
Apr 26, 2025 · 5 min read
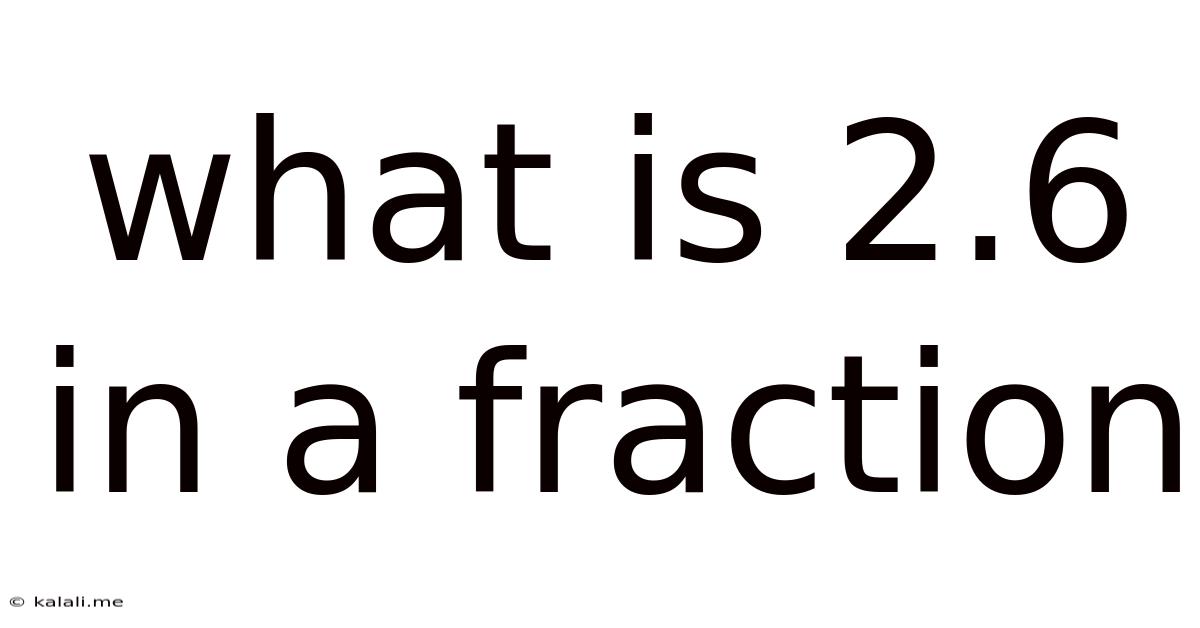
Table of Contents
What is 2.6 as a Fraction? A Comprehensive Guide
The seemingly simple question, "What is 2.6 as a fraction?", opens the door to a deeper understanding of decimal-to-fraction conversion, a fundamental skill in mathematics. This comprehensive guide will not only answer this specific question but also explore the underlying principles and provide you with the tools to convert any decimal number into its fractional equivalent. We'll cover various methods, address potential complexities, and even delve into the practical applications of this skill.
Understanding Decimals and Fractions
Before diving into the conversion process, let's refresh our understanding of decimals and fractions. A decimal is a number expressed in the base-10 system, using a decimal point to separate the whole number part from the fractional part. For example, in the number 2.6, '2' represents the whole number part, and '.6' represents the fractional part.
A fraction, on the other hand, represents a part of a whole and is expressed as a ratio of two integers – the numerator (top number) and the denominator (bottom number). The denominator indicates how many equal parts the whole is divided into, and the numerator indicates how many of those parts are being considered.
Converting 2.6 into a Fraction: The Basic Method
The most straightforward way to convert 2.6 into a fraction involves recognizing that the decimal part, '.6', represents six-tenths. Therefore, we can write 2.6 as a mixed number: 2 and 6/10.
This mixed number can then be converted into an improper fraction. To do this, we multiply the whole number (2) by the denominator (10), add the numerator (6), and keep the same denominator:
(2 * 10) + 6 = 26
So, 2.6 as an improper fraction is 26/10.
Simplifying the Fraction
The fraction 26/10 is not in its simplest form. To simplify a fraction, we need to find the greatest common divisor (GCD) of the numerator and the denominator. The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder. In this case, the GCD of 26 and 10 is 2.
Dividing both the numerator and the denominator by the GCD (2), we get:
26 ÷ 2 = 13 10 ÷ 2 = 5
Therefore, the simplest form of the fraction representing 2.6 is 13/5.
Alternative Methods for Decimal-to-Fraction Conversion
While the above method is the most common and intuitive for converting simple decimals, other methods can be employed, particularly for more complex decimal numbers.
-
Using Place Value: This method involves understanding the place value of each digit after the decimal point. In 2.6, the '6' is in the tenths place, meaning it represents 6/10. This directly gives us the fraction 2 and 6/10.
-
Multiplying by a Power of 10: For decimals with multiple digits after the decimal point, this method is very useful. To convert a decimal to a fraction, multiply both the numerator and the denominator by a power of 10 (10, 100, 1000, etc.) that eliminates the decimal point. For example, to convert 0.025 to a fraction:
Multiply by 1000: 0.025 * 1000 = 25 The denominator becomes 1000: 25/1000
Then simplify the fraction by finding the GCD of 25 and 1000 (which is 25):
25 ÷ 25 = 1 1000 ÷ 25 = 40
Therefore, 0.025 = 1/40.
-
Repeating Decimals: Converting repeating decimals (like 0.333...) to fractions requires a different approach. This involves setting up an equation and solving for x. For instance, to convert 0.333... to a fraction:
Let x = 0.333... Multiply by 10: 10x = 3.333... Subtract the first equation from the second: 10x - x = 3.333... - 0.333... This simplifies to 9x = 3 Solve for x: x = 3/9 = 1/3
Practical Applications of Decimal-to-Fraction Conversion
The ability to convert decimals to fractions is not just a theoretical exercise; it has many practical applications across various fields:
-
Cooking and Baking: Recipes often use fractions to measure ingredients. Understanding how to convert decimal measurements from digital scales to fractional equivalents ensures accuracy.
-
Construction and Engineering: Precise measurements are crucial in construction and engineering. Converting decimal measurements to fractions is essential for accurate calculations and blueprint interpretations.
-
Finance and Accounting: Working with percentages and proportions often requires converting decimals to fractions for calculations involving interest rates, discounts, and profit margins.
-
Data Analysis and Statistics: In data analysis, representing data as fractions can simplify calculations and provide a clearer understanding of proportions and relationships.
-
Science and Technology: Many scientific and technological calculations involve fractions. Converting decimal measurements to fractions can be necessary for precise calculations and data representation.
Advanced Considerations and Challenges
While converting simple decimals like 2.6 is straightforward, some situations present greater challenges:
-
Irrational Numbers: Irrational numbers like π (pi) and √2 (square root of 2) cannot be expressed as a simple fraction because they have infinite non-repeating decimal expansions. We can only use approximations in these cases.
-
Complex Decimals: Decimals with many digits after the decimal point or those with repeating patterns can require more complex calculation methods, often involving algebraic manipulation.
-
Significant Figures: When dealing with measurements, the concept of significant figures becomes important. The precision of the fraction should reflect the precision of the original decimal measurement.
Conclusion
Converting 2.6 to a fraction, as demonstrated, is a relatively straightforward process. However, the underlying principles and techniques discussed extend far beyond this specific example. Mastering decimal-to-fraction conversion provides a solid foundation for more advanced mathematical concepts and is a valuable skill applicable in numerous fields. By understanding the different methods and addressing the potential complexities, you can confidently tackle any decimal-to-fraction conversion task. Remember to always simplify your fractions to their lowest terms for the most accurate and concise representation.
Latest Posts
Latest Posts
-
What Is The Name Of The Covalent Compound Ccl4
Apr 26, 2025
-
How Many Grams Is 40 Mg
Apr 26, 2025
-
What Is A Quotient In Math Fractions
Apr 26, 2025
-
23 Out Of 35 As A Percentage
Apr 26, 2025
-
How Many Liters Are In 5000 Milliliters
Apr 26, 2025
Related Post
Thank you for visiting our website which covers about What Is 2.6 In A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.