What Is 2 To The 6th Power
Kalali
Mar 29, 2025 · 5 min read
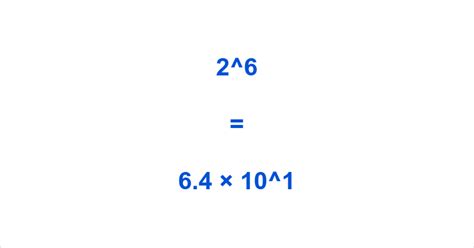
Table of Contents
What is 2 to the 6th Power? A Deep Dive into Exponents and Their Applications
The seemingly simple question, "What is 2 to the 6th power?" opens a door to a vast world of mathematical concepts, practical applications, and surprising connections. This article will not only answer that question but delve into the underlying principles of exponents, exploring their history, their use in various fields, and the broader implications of exponential growth.
Understanding Exponents: A Foundation in Mathematics
Before we tackle 2 to the 6th power, let's solidify our understanding of exponents. An exponent, also known as a power or index, indicates how many times a number (the base) is multiplied by itself. It's represented as a superscript number to the right of the base. For example, in the expression 2³, the '2' is the base, and the '3' is the exponent, signifying 2 multiplied by itself three times: 2 x 2 x 2 = 8.
Key Terminology:
- Base: The number being multiplied repeatedly.
- Exponent: The number indicating how many times the base is multiplied by itself.
- Power: Another term for exponent.
- Result: The final value obtained after performing the multiplication.
Calculating 2 to the 6th Power (2⁶)
Now, let's directly address the question: What is 2 to the 6th power? This means we need to multiply the base (2) by itself six times:
2⁶ = 2 x 2 x 2 x 2 x 2 x 2 = 64
Therefore, 2 to the 6th power is 64.
The Significance of Exponential Growth
The concept of raising a number to a power, particularly with a base greater than 1, illustrates exponential growth. This type of growth is characterized by a rapid increase in value over time. It's not a linear progression (adding a constant value each time) but rather a multiplicative one (multiplying by a constant value each time).
This characteristic of exponential growth is crucial in understanding various phenomena across multiple disciplines:
Examples of Exponential Growth in Real Life:
- Population Growth: Under ideal conditions, populations (human, animal, bacterial) can grow exponentially. A small initial population can quickly expand into a massive one.
- Compound Interest: The power of compound interest is a prime example of exponential growth. Earning interest on both your principal and accumulated interest leads to significant gains over time.
- Viral Spread: The spread of viral content (like videos or news stories) on social media often follows an exponential pattern. A few initial shares can quickly snowball into millions of views.
- Technological Advancement: Technological progress often exhibits exponential growth, with innovations building upon previous ones at an accelerating rate. Moore's Law, which describes the doubling of transistors on a microchip every two years, is a well-known example.
- Nuclear Chain Reactions: The rapid multiplication of neutrons in a nuclear chain reaction is another illustration of exponential growth, highlighting the immense power and potential dangers involved.
Beyond 2⁶: Exploring Different Exponents and Bases
While we've focused on 2⁶, the principles of exponents extend far beyond this specific example. Understanding different exponents and bases is crucial for comprehending more complex mathematical concepts.
Negative Exponents:
A negative exponent indicates a reciprocal. For example, 2⁻² is the same as 1/2² = 1/4. The negative sign essentially flips the base to the denominator of a fraction.
Fractional Exponents:
Fractional exponents represent roots. For example, 8^(1/3) is the cube root of 8, which is 2, because 2 x 2 x 2 = 8.
Zero Exponent:
Any number raised to the power of zero (except zero itself) equals 1. For example, 2⁰ = 1.
Larger Exponents:
As exponents get larger, the resulting values increase dramatically. Consider 2¹⁰ (1024) or 2²⁰ (over 1 million). This rapid increase is what makes exponential growth so significant.
Applications of Exponents in Different Fields
Exponents aren't confined to theoretical mathematics; they have extensive applications in various real-world fields:
Science and Engineering:
- Physics: Describing phenomena like radioactive decay, wave propagation, and the behavior of particles.
- Chemistry: Calculating reaction rates, concentrations, and the behavior of molecules.
- Computer Science: Analyzing algorithms, data structures, and computational complexity.
- Engineering: Designing structures, analyzing forces, and modeling complex systems.
Finance and Economics:
- Compound Interest: Calculating the future value of investments.
- Economic Growth: Modeling economic growth rates and predicting future economic trends.
- Financial Modeling: Developing sophisticated models for risk assessment and portfolio management.
Biology and Medicine:
- Population Dynamics: Modeling population growth and decline in various ecosystems.
- Epidemiology: Predicting the spread of infectious diseases.
- Pharmacokinetics: Understanding the absorption, distribution, metabolism, and excretion of drugs in the body.
Understanding Exponential Decay: The Counterpart to Exponential Growth
While exponential growth describes rapid increase, exponential decay describes rapid decrease. This is represented by a base between 0 and 1 raised to a power. For instance, (1/2)ⁿ represents a halving at each step. This is seen in:
- Radioactive decay: The rate at which radioactive materials lose their radioactivity.
- Drug metabolism: The rate at which the body eliminates drugs.
- Depreciation: The decrease in value of assets over time.
The Power of Logarithms: The Inverse of Exponentiation
Logarithms are the inverse operation of exponentiation. They answer the question: "To what power must the base be raised to obtain a specific value?" For instance, the logarithm base 2 of 64 (log₂64) is 6, because 2⁶ = 64. Logarithms are essential in various fields, including:
- Solving exponential equations: Finding unknown exponents.
- Analyzing data with large ranges: Compressing data for easier interpretation.
- Measuring sound intensity (decibels): A logarithmic scale that handles a wide range of sound pressures.
- Earthquake magnitude (Richter scale): Another logarithmic scale for measuring the intensity of earthquakes.
Conclusion: The Widespread Influence of Exponents
The seemingly simple question, "What is 2 to the 6th power?" leads us on a fascinating journey through the world of exponents. We've explored the fundamental principles, practical applications, and connections to broader mathematical concepts like logarithms and exponential growth and decay. The impact of exponents extends across diverse fields, highlighting their crucial role in understanding and modeling a vast array of real-world phenomena. From the growth of populations to the decay of radioactive materials, from financial investments to the spread of viral content, exponents provide a powerful tool for understanding the dynamics of our world. Hopefully, this in-depth exploration has enhanced your understanding and appreciation for this fundamental mathematical concept.
Latest Posts
Latest Posts
-
Why Does Passive Transport Not Require Energy
Apr 01, 2025
-
What Is 65 As A Fraction
Apr 01, 2025
-
How Many Miles Is 1600 Km
Apr 01, 2025
-
What Is 88 Cm In Inches
Apr 01, 2025
-
30 In Is How Many Feet
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about What Is 2 To The 6th Power . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
