What Is 24 Out Of 30 As A Percentage
Kalali
Mar 05, 2025 · 5 min read
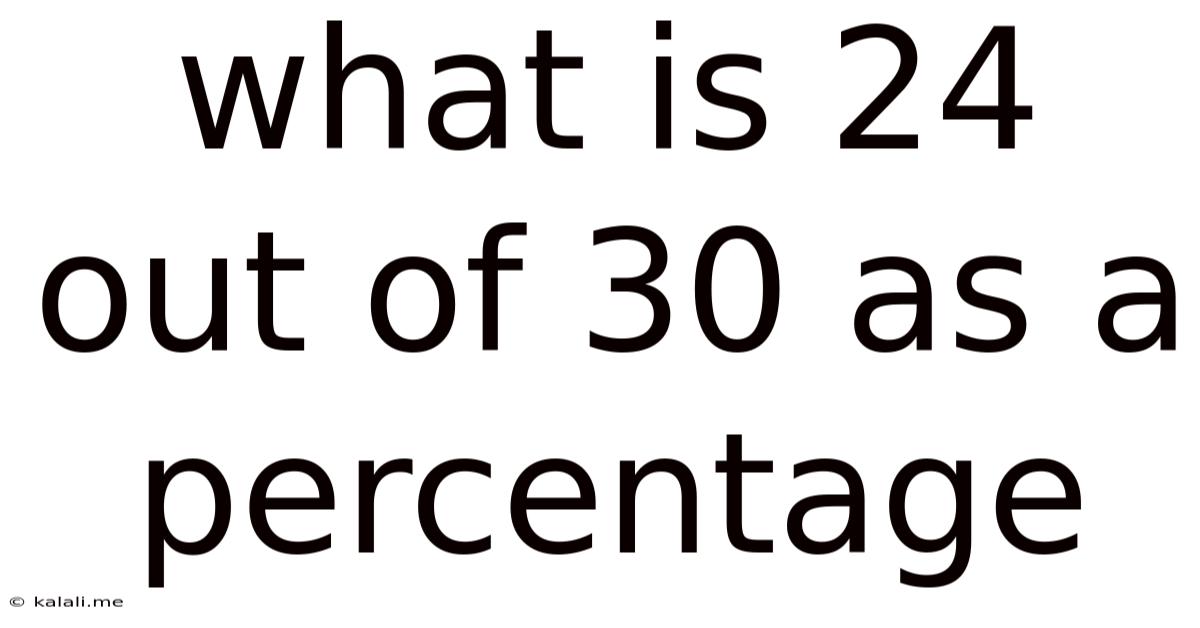
Table of Contents
What is 24 out of 30 as a Percentage? A Comprehensive Guide
Calculating percentages is a fundamental skill in various aspects of life, from academic studies to professional settings. Understanding how to convert fractions into percentages is crucial for interpreting data, making comparisons, and expressing proportions effectively. This comprehensive guide will delve into the process of determining what 24 out of 30 represents as a percentage, explaining the method step-by-step and exploring its practical applications.
Understanding Percentages
Before we dive into the calculation, let's solidify our understanding of percentages. A percentage is simply a fraction or ratio expressed as a part of 100. The symbol "%" represents "per cent," meaning "out of one hundred." For example, 50% means 50 out of 100, which is equivalent to ½ or 0.5.
Calculating 24 out of 30 as a Percentage: The Step-by-Step Method
To calculate what 24 out of 30 represents as a percentage, we follow a straightforward three-step process:
Step 1: Formulate the Fraction
The first step is to express the given information as a fraction. "24 out of 30" can be written as the fraction 24/30. The numerator (24) represents the part, and the denominator (30) represents the whole.
Step 2: Convert the Fraction to a Decimal
To convert the fraction 24/30 to a decimal, we divide the numerator by the denominator:
24 ÷ 30 = 0.8
Step 3: Convert the Decimal to a Percentage
Finally, to convert the decimal 0.8 to a percentage, we multiply it by 100 and add the percentage symbol (%):
0.8 x 100 = 80%
Therefore, 24 out of 30 is equal to 80%.
Alternative Calculation Method: Using Proportions
Another approach to solving this problem involves using proportions. We can set up a proportion to find the equivalent percentage:
24/30 = x/100
Here, 'x' represents the percentage we want to find. To solve for 'x', we cross-multiply:
30x = 2400
Then, divide both sides by 30:
x = 2400 ÷ 30 = 80
Therefore, x = 80%, confirming our previous calculation.
Practical Applications of Percentage Calculations
Understanding how to calculate percentages has numerous practical applications across diverse fields. Let's explore some examples:
1. Academic Performance
Imagine a student scored 24 out of 30 on a test. Knowing that this equates to 80%, the student can easily understand their performance relative to the total possible score. This allows for self-assessment and identification of areas needing improvement.
2. Sales and Discounts
Retail stores frequently offer discounts expressed as percentages. If a product is discounted by 20%, calculating the final price requires understanding percentage calculations. Similarly, calculating commission earned on sales also involves percentages.
3. Financial Calculations
Percentages play a vital role in various financial calculations, including interest rates, loan repayments, and investment returns. Understanding percentage calculations is essential for managing personal finances effectively.
4. Data Analysis and Interpretation
In data analysis, percentages are used extensively to represent proportions and trends within datasets. For instance, in market research, percentages are used to represent market share, customer satisfaction, and other key metrics.
5. Everyday Life
Percentages are encountered in various everyday situations, such as calculating tips in restaurants, determining the nutritional value of food, and understanding sales tax.
Simplifying Fractions for Easier Calculation
In many cases, simplifying the fraction before converting it to a decimal can make the calculation easier. Let's revisit the fraction 24/30. Both the numerator (24) and the denominator (30) are divisible by 6:
24 ÷ 6 = 4 30 ÷ 6 = 5
This simplifies the fraction to 4/5. Now, converting 4/5 to a decimal is simpler:
4 ÷ 5 = 0.8
Multiplying by 100 gives us the same result: 0.8 x 100 = 80%
Understanding the Concept of "Part" and "Whole"
A key concept in percentage calculations is understanding the relationship between the "part" and the "whole." The "part" is the value you're comparing to the "whole." In our example, 24 is the "part," and 30 is the "whole." Always ensure you're correctly identifying these two elements to avoid errors in your calculations.
Using Calculators and Spreadsheet Software
While the manual calculations are straightforward, utilizing calculators or spreadsheet software like Microsoft Excel or Google Sheets can significantly speed up the process, especially when dealing with more complex percentage calculations. These tools often have built-in functions specifically designed for percentage calculations, making the task more efficient.
Beyond the Basics: Advanced Percentage Calculations
While this article focuses on a basic percentage calculation, there are many advanced concepts in percentage calculations, such as:
- Percentage increase and decrease: Calculating the percentage change between two values.
- Percentage points: Representing the absolute difference between two percentages.
- Compound interest: Calculating interest earned on both principal and accumulated interest.
Mastering these advanced concepts will provide a more comprehensive understanding of percentages and their applications.
Conclusion: The Power of Percentage Calculations
Understanding how to calculate percentages, even something as seemingly simple as "What is 24 out of 30 as a percentage?", is a powerful skill applicable in countless situations. From academic success to financial management and professional settings, proficiency in percentage calculations is invaluable. By mastering this fundamental skill, you enhance your ability to analyze data, interpret information, and make informed decisions. Remember the three-step process outlined above: formulate the fraction, convert to a decimal, and then to a percentage. Practice regularly, and you'll soon find yourself effortlessly navigating the world of percentages.
Latest Posts
Latest Posts
-
What Is Half Of 1 1 2
Jul 03, 2025
-
How Much Do A Sandwich Bag Weigh
Jul 03, 2025
-
Why Did The Obtuse Angle Go To The Beach
Jul 03, 2025
-
How Much Is Three Quarts Of Water
Jul 03, 2025
-
How Tall Is A 3 Story Building
Jul 03, 2025
Related Post
Thank you for visiting our website which covers about What Is 24 Out Of 30 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.