What Is 25 Percent Of 15
Kalali
Apr 14, 2025 · 6 min read
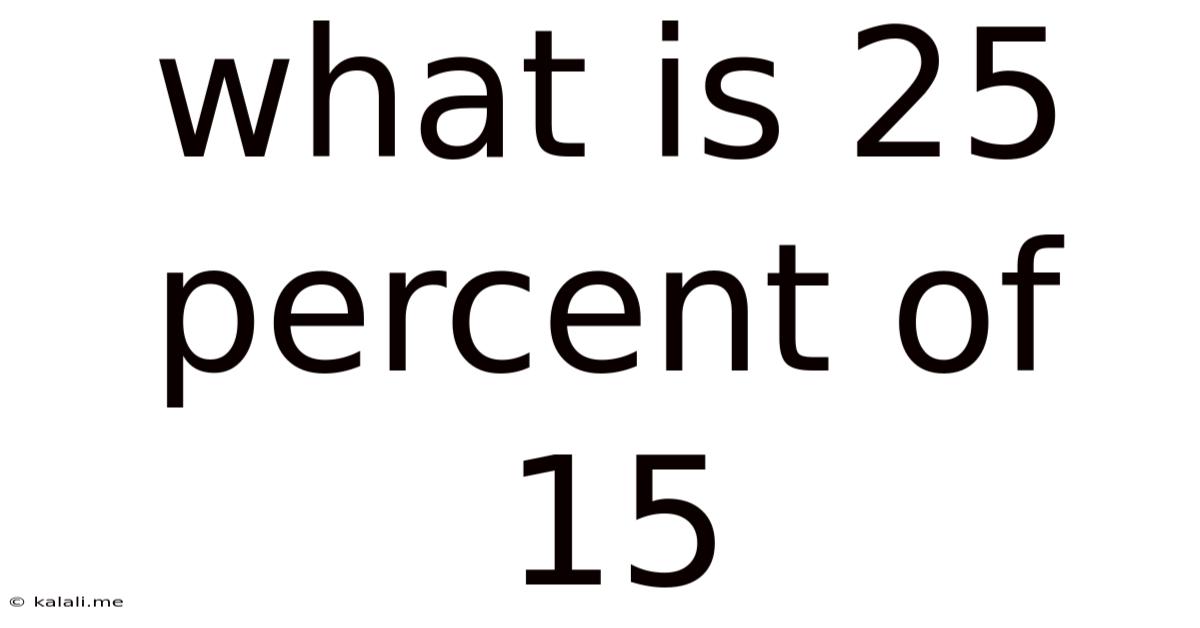
Table of Contents
What is 25 Percent of 15? A Deep Dive into Percentage Calculations and Their Applications
Finding 25 percent of 15 might seem like a simple arithmetic problem, easily solved with a calculator. However, understanding the underlying principles of percentage calculations is crucial for various applications in everyday life, from calculating discounts and tips to understanding financial reports and data analysis. This article will not only answer the initial question but will also explore the different methods to calculate percentages, their practical uses, and even delve into more complex percentage-related problems.
Meta Description: Learn how to calculate 25% of 15 and master percentage calculations. This comprehensive guide explores various methods, practical applications, and tackles more complex percentage problems, equipping you with essential mathematical skills.
The Simple Solution: Calculating 25% of 15
The most straightforward method to find 25% of 15 involves converting the percentage to a decimal and then multiplying it by the number. 25% can be written as 0.25 (by dividing 25 by 100). Therefore:
0.25 * 15 = 3.75
Therefore, 25% of 15 is 3.75. This is the quick and easy answer, but let's delve deeper into the "why" and explore alternative methods.
Understanding Percentages: The Foundation
A percentage is a fraction or a ratio expressed as a number out of 100. The term "percent" literally means "per hundred." Understanding this fundamental concept is key to mastering percentage calculations. When we say 25%, we mean 25 parts out of 100 equal parts. This can be represented as a fraction (25/100) or a decimal (0.25).
This representation allows for easy conversion between percentages, fractions, and decimals. This flexibility is crucial in various mathematical operations and real-world applications.
Alternative Methods for Calculating Percentages
While the decimal method is efficient, other methods offer different perspectives and can be helpful depending on the complexity of the problem:
-
Fraction Method: 25% can be expressed as the fraction ¼ (25/100 simplified). Therefore, finding 25% of 15 is equivalent to finding ¼ of 15. This can be calculated as 15 ÷ 4 = 3.75. This method is particularly useful when dealing with percentages that have easy fractional equivalents, such as 50% (½), 75% (¾), and 10% (1/10).
-
Proportion Method: This method uses the concept of ratios. We can set up a proportion:
25/100 = x/15
Cross-multiplying gives: 100x = 25 * 15
Solving for x: x = (25 * 15) / 100 = 3.75
This method is helpful for visualizing the relationship between the percentage and the whole number.
Practical Applications of Percentage Calculations
Percentage calculations are ubiquitous in our daily lives. Here are some examples:
-
Discounts and Sales: Stores frequently offer discounts expressed as percentages. Understanding percentage calculations allows you to quickly determine the final price after a discount. For example, a 20% discount on a $50 item means a reduction of $10 (20% of $50), resulting in a final price of $40.
-
Taxes: Sales tax is usually expressed as a percentage. Calculating the total cost of an item including tax requires adding the tax percentage to the original price. For instance, a 6% sales tax on a $100 item adds $6 (6% of $100), bringing the total cost to $106.
-
Tips and Gratuities: When dining out, it’s customary to leave a tip, usually expressed as a percentage of the bill. Calculating the tip amount involves finding the percentage of the total bill. For example, a 15% tip on a $75 bill amounts to $11.25 (15% of $75).
-
Interest Rates: Understanding percentage calculations is crucial when dealing with interest rates on loans, savings accounts, and investments. Interest is usually calculated as a percentage of the principal amount.
-
Financial Reports: Financial statements, such as income statements and balance sheets, often use percentages to represent various financial ratios and metrics. Analyzing these percentages helps in understanding the financial health and performance of a company.
-
Data Analysis: Percentages are widely used in data analysis to represent proportions and changes over time. They provide a standardized way to compare different datasets and identify trends. For example, comparing the percentage change in sales from one year to the next.
-
Scientific Calculations: Percentages are also used in scientific fields like chemistry, physics, and biology to express concentrations, error margins, and other quantitative measurements.
More Complex Percentage Problems
While finding 25% of 15 is relatively straightforward, let's explore more complex scenarios that build upon the fundamental principles we've covered:
Scenario 1: Finding the original value after a percentage increase.
Suppose a product's price increased by 10% to $66. What was the original price?
Let's denote the original price as 'x'. A 10% increase means the final price is 110% of the original price (100% + 10%). We can set up the equation:
1.10x = 66
Solving for x: x = 66 / 1.10 = $60
Therefore, the original price was $60.
Scenario 2: Finding the percentage change between two values.
Suppose sales increased from $500 to $600. What is the percentage increase?
First, find the difference between the two values: $600 - $500 = $100
Next, divide the difference by the original value: $100 / $500 = 0.20
Finally, multiply by 100 to express the result as a percentage: 0.20 * 100 = 20%
Therefore, the percentage increase in sales is 20%.
Scenario 3: Calculating multiple percentage changes.
Imagine a 20% increase followed by a 10% decrease. Does this result in a net change of 10%? Not quite. Let's illustrate with an example.
Start with a value of $100.
20% increase: $100 + ($100 * 0.20) = $120
10% decrease on the new value: $120 - ($120 * 0.10) = $108
The net change is an 8% increase, not a 10% change. This highlights the importance of calculating percentage changes sequentially and not simply adding or subtracting percentages directly.
Mastering Percentage Calculations: Tips and Practice
Mastering percentage calculations requires consistent practice and a solid understanding of the underlying concepts. Here are some tips to improve your skills:
-
Practice regularly: Solve various percentage problems of different complexities to build your confidence and proficiency.
-
Use different methods: Experiment with different approaches (decimal, fraction, proportion) to find the method that best suits your understanding and the problem at hand.
-
Visualize the problem: Try to visualize the problem using diagrams or charts to better grasp the relationship between the percentage, the part, and the whole.
-
Check your work: Always double-check your calculations to ensure accuracy.
-
Utilize online resources: Numerous online calculators and tutorials are available to help you practice and reinforce your understanding.
By understanding the fundamentals and applying the methods discussed, you can confidently tackle various percentage-related problems in your daily life, academic pursuits, and professional endeavors. Remember that the seemingly simple question, "What is 25% of 15?" opens the door to a vast world of mathematical applications and problem-solving skills.
Latest Posts
Latest Posts
-
A Bunch Of Amino Acids Attached Together Is Called A
Apr 15, 2025
-
Temperature At Which Water Vapor Condenses
Apr 15, 2025
-
What Is 14 20 As A Percentage
Apr 15, 2025
-
What Percent Of 75 Is 33
Apr 15, 2025
-
60 Is What Percent Of 25
Apr 15, 2025
Related Post
Thank you for visiting our website which covers about What Is 25 Percent Of 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.