What Is 25 Percent Of 8
Kalali
Apr 18, 2025 · 5 min read
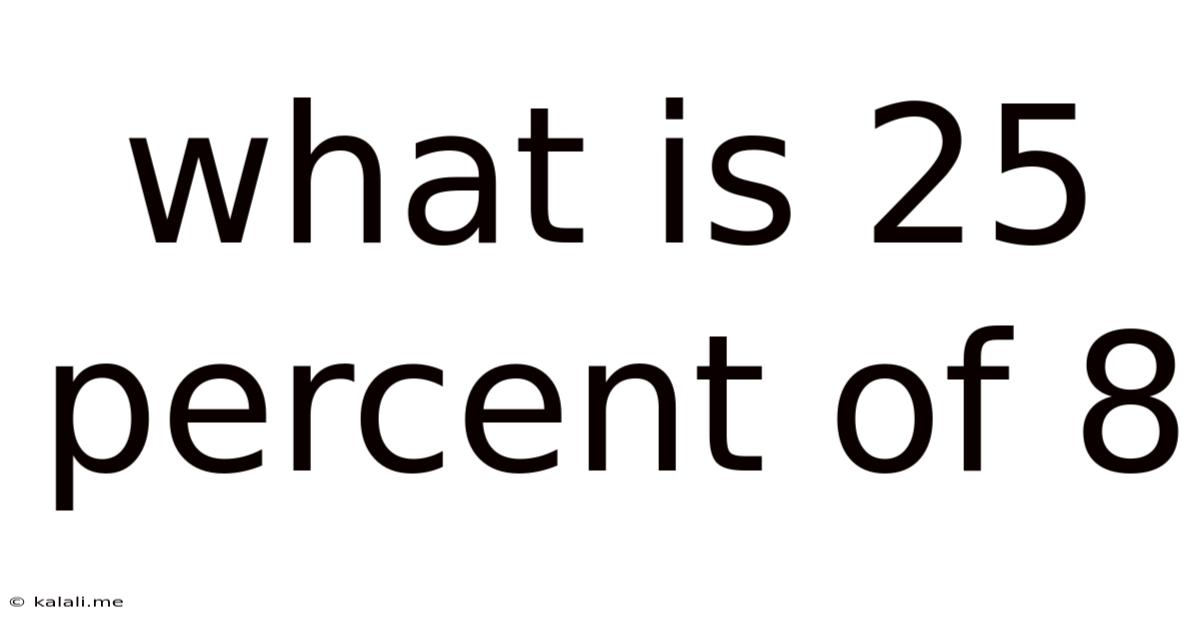
Table of Contents
What is 25 Percent of 8? A Deep Dive into Percentages and Their Applications
This seemingly simple question, "What is 25 percent of 8?", opens the door to a fascinating exploration of percentages, their practical applications, and the underlying mathematical principles. While the answer itself is straightforward, understanding the how and why behind the calculation is crucial for anyone wanting to confidently tackle percentage problems in various real-world scenarios. This article will not only provide the solution but delve into the multiple ways to calculate percentages, their significance in everyday life, and even touch upon advanced applications in fields like finance and statistics.
Meta Description: Learn how to calculate 25% of 8 and master percentage calculations. This comprehensive guide explores different methods, real-world applications, and advanced percentage concepts for a thorough understanding.
Understanding Percentages: The Basics
A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per cent" or "out of 100." So, 25% means 25 out of 100, which can be written as the fraction 25/100 or the decimal 0.25. This fundamental understanding is key to solving any percentage problem.
Calculating 25% of 8: Three Proven Methods
There are several ways to calculate 25% of 8. Let's explore three common methods:
Method 1: Using the Fraction Equivalent
As mentioned, 25% is equivalent to the fraction 25/100. To find 25% of 8, we simply multiply 8 by the fraction 25/100:
8 * (25/100) = 200/100 = 2
Therefore, 25% of 8 is 2.
Method 2: Using Decimal Equivalents
We can also convert the percentage to its decimal equivalent. Since 25% = 0.25, we can calculate:
8 * 0.25 = 2
Again, the answer is 2. This method is often preferred for its simplicity and ease of use with calculators.
Method 3: Using Proportions
This method is particularly useful for understanding the underlying relationship between percentages and proportions. We can set up a proportion:
25/100 = x/8
where 'x' represents the unknown value (25% of 8). To solve for x, we cross-multiply:
100x = 25 * 8 100x = 200 x = 200/100 x = 2
Once again, we find that 25% of 8 is 2.
Real-World Applications of Percentage Calculations
Understanding percentages is vital in numerous everyday situations:
- Shopping: Calculating discounts, sales tax, and tip amounts. For example, a 25% discount on an $8 item would result in a savings of $2.
- Finance: Determining interest rates on loans and savings accounts, calculating profit margins, and understanding investment returns.
- Statistics: Analyzing data, interpreting survey results, and understanding probability. Percentages are used to represent proportions within larger datasets.
- Science: Expressing concentrations of solutions, measuring experimental yields, and representing statistical significance.
- Everyday Life: Understanding nutritional information on food labels (percentage of daily value), calculating grades in school, and even figuring out the tip at a restaurant.
Beyond the Basics: Advanced Percentage Concepts
While calculating 25% of 8 is relatively simple, a deeper understanding of percentages opens up a world of more complex calculations and applications:
- Percentage Increase and Decrease: This involves calculating the percentage change between two values. For instance, if a price increases from $8 to $10, the percentage increase is calculated as [(10-8)/8] * 100% = 25%.
- Compound Interest: This involves calculating interest on both the principal amount and accumulated interest over time. It's a crucial concept in finance and investment.
- Percentage Points: It's crucial to differentiate between percentage change and percentage points. A change from 20% to 25% is a 5 percentage point increase, but a 25% increase from 20%.
- Weighted Averages: Calculating weighted averages using percentages is essential in many fields, including finance and academics. This involves assigning different weights to different values based on their importance or contribution.
Solving More Complex Percentage Problems
Let's explore some more complex examples to solidify your understanding:
Example 1: Finding the original value.
If 25% of a number is 6, what is the number?
We can set up the equation: 0.25x = 6. Solving for x, we get x = 6 / 0.25 = 24. The original number is 24.
Example 2: Calculating percentage increase.
A store increases the price of an item from $8 to $12. What is the percentage increase?
The increase is $12 - $8 = $4. The percentage increase is ($4/$8) * 100% = 50%.
Example 3: Calculating percentage decrease.
An item originally priced at $20 is discounted to $15. What is the percentage decrease?
The decrease is $20 - $15 = $5. The percentage decrease is ($5/$20) * 100% = 25%.
Tips for Mastering Percentage Calculations
- Practice regularly: The more you practice, the more comfortable you'll become with different types of percentage problems.
- Understand the concepts: Don't just memorize formulas; understand the underlying principles.
- Use different methods: Try different methods to solve the same problem to find the approach that works best for you.
- Check your answers: Always double-check your calculations to ensure accuracy.
- Utilize online resources: There are many online resources available to help you practice and learn more about percentages.
Conclusion: The Power of Percentages
While seemingly simple, the question "What is 25 percent of 8?" opens the door to a vast and important area of mathematics with widespread real-world applications. Mastering percentage calculations empowers you to confidently navigate various situations, from everyday shopping to complex financial analyses. This article has provided not only the solution but also a comprehensive understanding of the underlying principles and advanced applications, enabling you to tackle percentage problems with increased confidence and proficiency. Remember to practice consistently and explore the numerous online resources available to further enhance your understanding and skill in this fundamental area of mathematics.
Latest Posts
Latest Posts
-
Is Eubacteria Single Celled Or Multicellular
Apr 19, 2025
-
3 5 Feet Is How Many Inches
Apr 19, 2025
-
3 Out Of 13 As A Percentage
Apr 19, 2025
-
Which Statement Describes An Atomic Nucleus
Apr 19, 2025
-
What Is A Factor Of 56
Apr 19, 2025
Related Post
Thank you for visiting our website which covers about What Is 25 Percent Of 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.