What Is 3/15 As A Percent
Kalali
Mar 27, 2025 · 5 min read
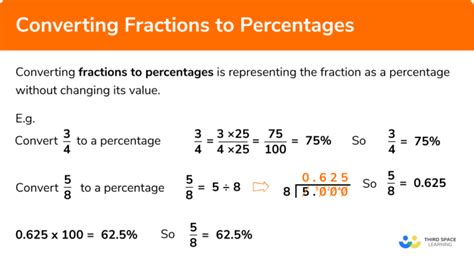
Table of Contents
What is 3/15 as a Percent? A Comprehensive Guide to Fraction-to-Percentage Conversion
Converting fractions to percentages is a fundamental skill in mathematics with widespread applications in everyday life, from calculating discounts and sales tax to understanding statistical data and financial reports. This comprehensive guide will delve into the process of converting the fraction 3/15 into a percentage, explaining the underlying concepts and providing practical examples to solidify your understanding. We'll explore multiple methods, ensuring you grasp the core principles and can confidently tackle similar conversions in the future.
Understanding Fractions and Percentages
Before diving into the conversion, let's briefly revisit the definitions of fractions and percentages.
-
Fraction: A fraction represents a part of a whole. It is expressed as a ratio of two numbers, the numerator (top number) and the denominator (bottom number). In the fraction 3/15, 3 is the numerator and 15 is the denominator. This means we have 3 parts out of a total of 15 parts.
-
Percentage: A percentage is a way of expressing a number as a fraction of 100. The symbol % represents "per cent," meaning "out of 100." For example, 50% means 50 out of 100, or 50/100.
Method 1: Simplifying the Fraction
The simplest and often most efficient method to convert a fraction to a percentage involves simplifying the fraction first. This makes the subsequent conversion to a percentage much easier.
-
Find the Greatest Common Divisor (GCD): The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder. In the case of 3/15, the GCD is 3.
-
Simplify the Fraction: Divide both the numerator and the denominator by the GCD.
3/15 ÷ 3/3 = 1/5
-
Convert the Simplified Fraction to a Decimal: Divide the numerator (1) by the denominator (5).
1 ÷ 5 = 0.2
-
Convert the Decimal to a Percentage: Multiply the decimal by 100 and add the percentage symbol (%).
0.2 x 100 = 20%
Therefore, 3/15 simplifies to 1/5, which is equivalent to 20%.
Method 2: Direct Conversion from Fraction to Percentage
This method involves a direct calculation without simplifying the fraction beforehand. While it might seem longer, it reinforces the underlying concept of percentages as parts of 100.
-
Set up the Proportion: We want to find the percentage equivalent of 3/15. We can set up a proportion:
3/15 = x/100
Where 'x' represents the percentage we're trying to find.
-
Cross-Multiply: To solve for 'x', we cross-multiply:
15x = 300
-
Solve for x: Divide both sides by 15:
x = 300/15 = 20
-
Add the Percentage Symbol: Therefore, x = 20%, confirming our earlier result.
Method 3: Using a Calculator
Modern calculators are equipped to handle fraction-to-percentage conversions seamlessly. Simply enter the fraction 3/15 and convert it to a percentage using the calculator's built-in functions. This method is quick and convenient, particularly for more complex fractions. However, understanding the underlying mathematical principles, as shown in the previous methods, is crucial for developing a strong mathematical foundation.
Real-World Applications of Fraction-to-Percentage Conversions
The ability to convert fractions to percentages has numerous practical applications in various fields:
-
Finance: Calculating interest rates, discounts, profit margins, and tax rates all involve converting fractions to percentages. For example, a 1/4 discount on an item means a 25% discount.
-
Statistics: Percentages are used extensively to represent data in charts, graphs, and reports. Converting fractions representing proportions within a dataset to percentages allows for easier interpretation and comparison.
-
Retail: Sales and discounts are often expressed as percentages. Converting fractional discounts to percentages helps customers quickly understand the savings.
-
Science: Percentages are commonly used to express concentrations, yields, and errors in experimental results.
-
Everyday Life: Calculating tips, understanding nutritional information on food labels, and interpreting survey results all involve working with percentages.
Expanding on the Concept: Working with More Complex Fractions
While 3/15 is a relatively simple fraction, the principles discussed here can be applied to more complex fractions. The key is to simplify the fraction whenever possible before converting it to a decimal and then a percentage. For example, let's consider the fraction 17/68:
-
Find the GCD: The GCD of 17 and 68 is 17.
-
Simplify: 17/68 ÷ 17/17 = 1/4
-
Convert to Decimal: 1 ÷ 4 = 0.25
-
Convert to Percentage: 0.25 x 100 = 25%
Therefore, 17/68 is equivalent to 25%.
Addressing Potential Errors and Common Mistakes
When converting fractions to percentages, common errors can arise from:
-
Incorrect Simplification: Failing to find the greatest common divisor can lead to inaccurate results. Always ensure the fraction is simplified to its lowest terms before proceeding.
-
Decimal Errors: Mistakes in converting the simplified fraction to a decimal can also affect the final percentage. Double-check your calculations to avoid errors.
-
Misunderstanding Percentage Meaning: Remember that a percentage represents a fraction out of 100. This is the fundamental concept that governs the conversion process.
Conclusion: Mastering Fraction-to-Percentage Conversions
Converting fractions to percentages is a critical skill with wide-ranging applications. By mastering the methods outlined above, you'll be well-equipped to confidently handle these conversions in various contexts. Remember to practice regularly, utilize the different methods, and always double-check your calculations to avoid errors. Understanding the underlying principles, beyond simply using a calculator, will strengthen your mathematical skills and allow you to tackle more complex problems efficiently and accurately. With practice and a clear understanding of the concepts, you can confidently navigate the world of fractions and percentages.
Latest Posts
Latest Posts
-
1 Cup Of Sour Cream In Oz
Mar 30, 2025
-
Cuanto Es El 30 De 50
Mar 30, 2025
-
Spent Lead Acid Batteries Are Exempt From Hazardous Waste
Mar 30, 2025
-
How Many Centimeters Is 21 In
Mar 30, 2025
-
How Many Ounces Equals 2 Pounds
Mar 30, 2025
Related Post
Thank you for visiting our website which covers about What Is 3/15 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
