What Is 3 To The Power Of 3
Kalali
Apr 09, 2025 · 5 min read
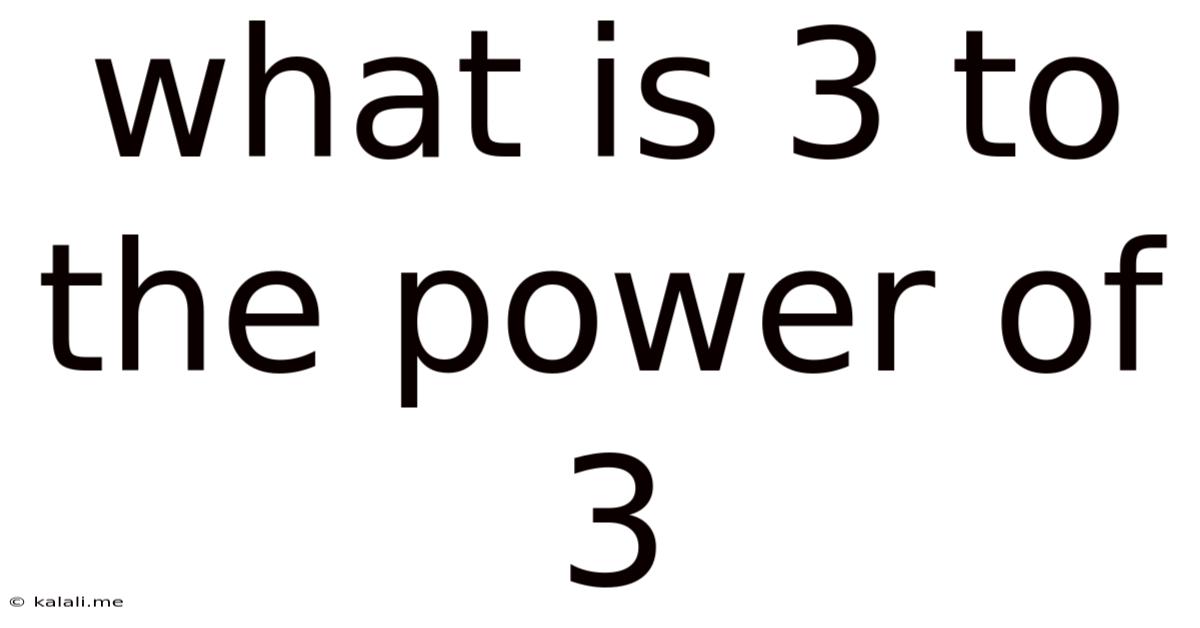
Table of Contents
What is 3 to the Power of 3? A Deep Dive into Exponentiation and its Applications
What is 3 to the power of 3? The seemingly simple question belies a deeper exploration into the world of exponentiation, a fundamental concept in mathematics with far-reaching applications across various fields. This article will not only answer the initial question but delve into the mechanics of exponentiation, its practical uses, and related mathematical concepts. Understanding exponents is crucial for anyone venturing into higher-level mathematics, computer science, finance, and even everyday problem-solving.
3 to the power of 3, denoted as 3³, is simply 3 multiplied by itself three times: 3 x 3 x 3 = 27. This is the straightforward answer. However, let's unpack the broader implications of this seemingly simple calculation.
Understanding Exponentiation: The Basics
Exponentiation, often referred to as "raising to a power," is a mathematical operation involving two numbers: the base and the exponent. The base is the number being multiplied, and the exponent (or power) indicates how many times the base is multiplied by itself. In the case of 3³, 3 is the base, and 3 is the exponent.
The general form of exponentiation is: bⁿ, where 'b' is the base and 'n' is the exponent. This represents 'b' multiplied by itself 'n' times.
Examples:
- 2⁴ = 2 x 2 x 2 x 2 = 16
- 5² = 5 x 5 = 25
- 10¹ = 10
- 7⁰ = 1 (Any non-zero number raised to the power of 0 is 1)
Beyond the Basics: Negative and Fractional Exponents
The concept of exponentiation extends beyond positive integers. We can also have negative and fractional exponents:
-
Negative Exponents: A negative exponent indicates the reciprocal of the base raised to the positive exponent. For example:
- 3⁻² = 1/3² = 1/(3 x 3) = 1/9
- x⁻ⁿ = 1/xⁿ
-
Fractional Exponents: A fractional exponent represents a root. For example:
- 8^(1/3) = ∛8 = 2 (The cube root of 8)
- x^(m/n) = (ⁿ√x)ᵐ (The nth root of x, raised to the power of m)
Properties of Exponents
Understanding the properties of exponents is essential for simplifying expressions and solving equations:
- Product of Powers: When multiplying two numbers with the same base, you add the exponents: xᵐ * xⁿ = x^(m+n)
- Quotient of Powers: When dividing two numbers with the same base, you subtract the exponents: xᵐ / xⁿ = x^(m-n)
- Power of a Power: When raising a power to another power, you multiply the exponents: (xᵐ)ⁿ = x^(m*n)
- Power of a Product: When raising a product to a power, you raise each factor to that power: (xy)ⁿ = xⁿyⁿ
- Power of a Quotient: When raising a quotient to a power, you raise both the numerator and the denominator to that power: (x/y)ⁿ = xⁿ/yⁿ
Applications of Exponentiation
Exponentiation is not just a theoretical concept; it has widespread practical applications across numerous fields:
-
Compound Interest: In finance, compound interest calculations rely heavily on exponents. The formula A = P(1 + r/n)^(nt) calculates the future value (A) of an investment based on the principal amount (P), interest rate (r), number of times interest is compounded per year (n), and the number of years (t).
-
Exponential Growth and Decay: Exponentiation is fundamental to modeling exponential growth (e.g., population growth, bacterial growth) and exponential decay (e.g., radioactive decay, drug metabolism). These processes are described by equations of the form y = abˣ, where 'a' is the initial value, 'b' is the growth/decay factor, and 'x' is the time.
-
Computer Science: Exponentiation is crucial in computer algorithms and data structures. Bit manipulation, hashing functions, and computational complexity analysis often involve exponential calculations. Binary numbers, the foundation of digital computing, are essentially representations of numbers using powers of 2.
-
Physics and Engineering: Many physical phenomena, such as the intensity of light, sound waves, and radioactive decay, follow exponential relationships. Exponential functions are also used in modeling various engineering problems.
-
Probability and Statistics: Exponential distributions are used extensively in probability and statistics to model the time until an event occurs in a Poisson process. They're crucial in fields like queuing theory and reliability analysis.
-
Biology: Exponential growth is a key concept in understanding population dynamics and the spread of diseases. Models using exponential functions can help predict population sizes and the trajectory of epidemics.
-
Chemistry: Exponential relationships are encountered in chemical kinetics, describing the rate of chemical reactions.
Connecting 3³ to Larger Mathematical Concepts
Understanding 3³ allows us to explore more advanced mathematical concepts:
-
Polynomial Equations: Expressions involving exponents, like 3³, are fundamental building blocks of polynomials. Solving polynomial equations often requires manipulating and simplifying expressions containing exponents.
-
Calculus: The concept of exponents is vital in calculus, specifically in differentiation and integration. Derivatives and integrals of exponential functions are crucial for solving numerous problems in physics, engineering, and other fields.
-
Number Theory: Number theory, a branch of mathematics dealing with integers and their properties, makes significant use of exponents in concepts like modular arithmetic and Fermat's Little Theorem.
Solving Problems Involving 3³
Let's consider some examples that involve 3³:
Example 1: A cube has sides of length 3 cm. What is its volume?
The volume of a cube is calculated as side³. Therefore, the volume is 3³ = 27 cubic centimeters.
Example 2: A bacteria population triples every hour. If you start with 1 bacterium, how many will you have after 3 hours?
After 1 hour: 1 x 3 = 3 bacteria After 2 hours: 3 x 3 = 9 bacteria After 3 hours: 9 x 3 = 27 bacteria (This can also be calculated as 1 x 3³ = 27)
Example 3: Simplify the expression: (3²)³
Using the power of a power rule, this simplifies to 3^(2*3) = 3⁶ = 729.
Conclusion: The Significance of 3³ and Exponentiation
While the answer to "What is 3 to the power of 3?" is simply 27, the true value lies in understanding the broader context of exponentiation. This fundamental mathematical operation underpins numerous applications across various disciplines. Mastering the concepts of exponents, their properties, and their application to real-world problems is essential for anyone seeking a deeper understanding of mathematics and its impact on the world around us. From calculating compound interest to modeling population growth and understanding the intricacies of computer algorithms, exponentiation proves itself to be a powerful and ubiquitous tool. The seemingly simple calculation of 3³ serves as a gateway to a vast and fascinating landscape of mathematical knowledge.
Latest Posts
Latest Posts
-
71 Inches Is How Many Cm
Apr 17, 2025
-
13 3 As A Mixed Number
Apr 17, 2025
-
How Is Photosynthesis And Cellular Respiration Different
Apr 17, 2025
-
What Is 5 2 In Meters
Apr 17, 2025
-
What Is 2 3 Cup 2 3 Cup
Apr 17, 2025
Related Post
Thank you for visiting our website which covers about What Is 3 To The Power Of 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.