What Is 30 Percent Of 000
Kalali
Apr 09, 2025 · 5 min read
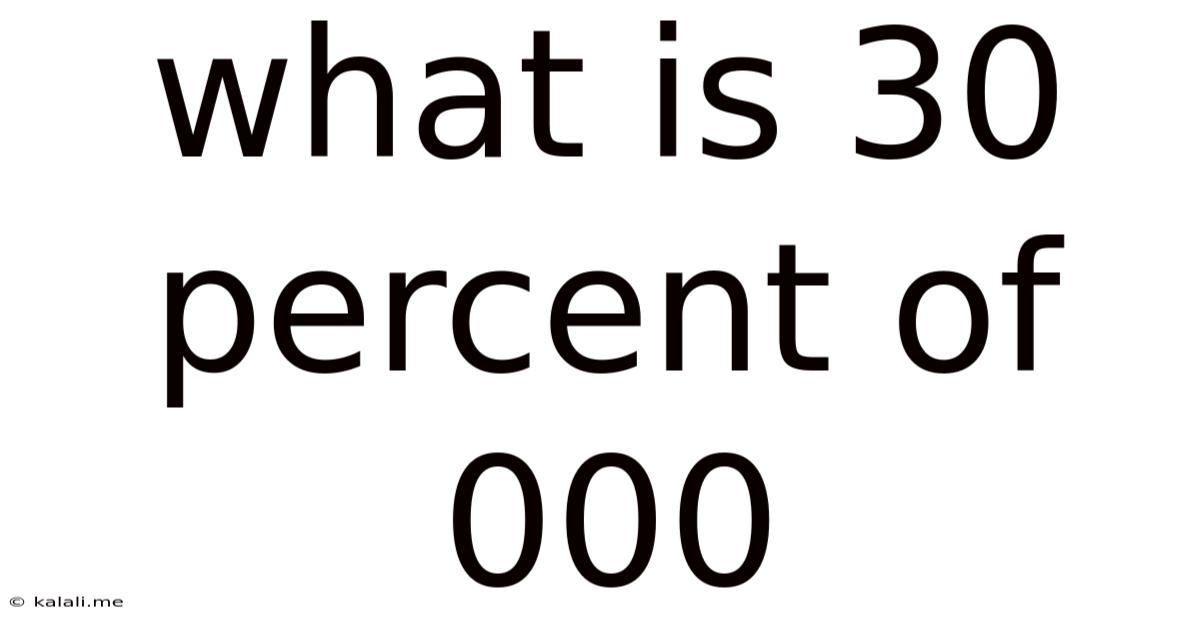
Table of Contents
What is 30 Percent of 0? Understanding Percentage Calculations and Zero
This seemingly simple question, "What is 30 percent of 0?", actually opens a door to understanding fundamental concepts in mathematics, particularly percentages and their application in various scenarios. While the answer itself is straightforward, exploring the underlying principles enhances our grasp of percentage calculations and their significance in real-world problems. This article will not only answer the question directly but also delve into the broader context of percentage calculations, especially those involving zero.
Meta Description: Discover the answer to "What is 30 percent of 0?" and learn the underlying principles of percentage calculations, including how zero impacts these calculations. Explore real-world applications and common misconceptions surrounding percentages.
Understanding Percentages: A Quick Refresher
Before tackling the specific problem, let's briefly review the concept of percentages. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "per cent," meaning "out of one hundred." For example, 50% means 50 out of 100, which simplifies to 1/2 or 0.5.
Calculating a percentage of a number involves multiplying the number by the percentage expressed as a decimal. To convert a percentage to a decimal, simply divide the percentage by 100. For instance, 30% becomes 0.30 (or 0.3).
Calculating 30 Percent of 0
Now, let's address the core question: What is 30 percent of 0?
The calculation is simple: 0.30 * 0 = 0
Therefore, 30 percent of 0 is 0.
This result might seem obvious, but it's crucial to understand why this is the case. Multiplication by zero always results in zero. Regardless of the percentage, if the base number is zero, the result of the percentage calculation will always be zero.
Zero in Percentage Calculations: Implications and Applications
The role of zero in percentage calculations is often overlooked but holds significant practical implications. Understanding these implications helps us avoid errors and interpret results correctly in various contexts.
-
Financial Calculations: In finance, zero often represents a starting point or a lack of capital. Calculating a percentage of zero could represent scenarios like:
- No initial investment: If someone invests zero dollars, then any percentage return on that investment will also be zero.
- Zero profit margin: A product with zero profit margin means that any percentage markup or discount will still result in zero profit.
- Zero debt: Calculating interest on zero debt will naturally result in zero interest payment.
-
Data Analysis and Statistics: In data analysis and statistics, zero often represents the absence of a particular attribute or characteristic. For example:
- Zero defects: If a production line reports zero defects, then the percentage of defects is, of course, zero.
- Zero responses: A survey with zero responses indicates that no percentage can be calculated for specific preferences or demographics.
- Zero growth: A business experiencing zero growth indicates that any percentage growth calculation will be zero.
-
Scientific Calculations and Measurement: Zero is an integral part of scientific measurements and calculations. It indicates the absence of a quantity or a starting point.
- Zero temperature: Certain temperature scales (like Kelvin) use zero to represent the absence of thermal energy. Percentage calculations concerning temperature changes from absolute zero would always yield zero.
- Zero velocity: An object at rest has a velocity of zero, and any percentage change in its velocity would remain zero.
Addressing Common Misconceptions
While the calculation of 30% of 0 is straightforward, some misconceptions can arise when dealing with percentages and zero:
-
Misinterpretation of Zero as 'Nothing': While zero represents the absence of quantity, it's not simply 'nothing.' It's a crucial numerical value that plays a vital role in mathematical operations. It's essential to treat zero with the same mathematical rigor as any other number.
-
Confusion with Undefined Percentages: One might mistakenly assume that a percentage of zero is undefined. However, this is not the case. It's perfectly well-defined and always equals zero.
-
Ignoring Zero in Calculations: In complex calculations, it's easy to overlook a zero value, which can lead to errors. Always ensure that all relevant data, including zeroes, are considered in the calculation.
Expanding the Understanding of Percentages: Advanced Concepts
Moving beyond the basics, let's explore more advanced aspects of percentage calculations:
-
Percentage Increase and Decrease: Understanding percentage changes is crucial in many areas. A percentage increase is calculated as [(New Value - Old Value) / Old Value] * 100. A percentage decrease is calculated similarly, but the result is negative. Note that calculating percentage change when the old value is zero results in an undefined value.
-
Compounding Percentages: Compounding involves applying percentages repeatedly over time. For instance, calculating compound interest. However, in such calculations, an initial value of zero will always result in a final value of zero irrespective of the compounding periods.
-
Weighted Averages and Percentages: In statistics, weighted averages involve assigning weights to different values. If one of the values is zero, its weighted contribution to the average will also be zero, affecting the overall result.
-
Percentage Points vs. Percentage Change: It's important to differentiate between percentage points and percentage change. A percentage point refers to an absolute change in percentage terms (e.g., from 10% to 20% is a 10 percentage point increase), while a percentage change represents a relative change.
Conclusion
The seemingly trivial question of "What is 30 percent of 0?" provides a solid foundation for understanding percentage calculations and the role of zero in various contexts. While the answer is simply 0, the underlying principles highlight the importance of careful consideration of zero in mathematical operations, particularly when dealing with financial calculations, data analysis, and scientific measurements. A firm understanding of percentage calculation, including its application with zero, enhances our ability to interpret data, solve problems, and make informed decisions in various aspects of life. Remember, even seemingly simple calculations can unlock deeper mathematical understanding and practical applications.
Latest Posts
Latest Posts
-
Velocidad De Escape De La Tierra En Km H
Apr 18, 2025
-
Least Common Multiple Of 7 And 11
Apr 18, 2025
-
What Are Indicators That A Chemical Reaction Has Occurred
Apr 18, 2025
-
What Percentage Is 5 Out Of 12
Apr 18, 2025
-
1 5 Ounces Is How Many Grams
Apr 18, 2025
Related Post
Thank you for visiting our website which covers about What Is 30 Percent Of 000 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.