What Percentage Is 5 Out Of 12
Kalali
Apr 18, 2025 · 5 min read
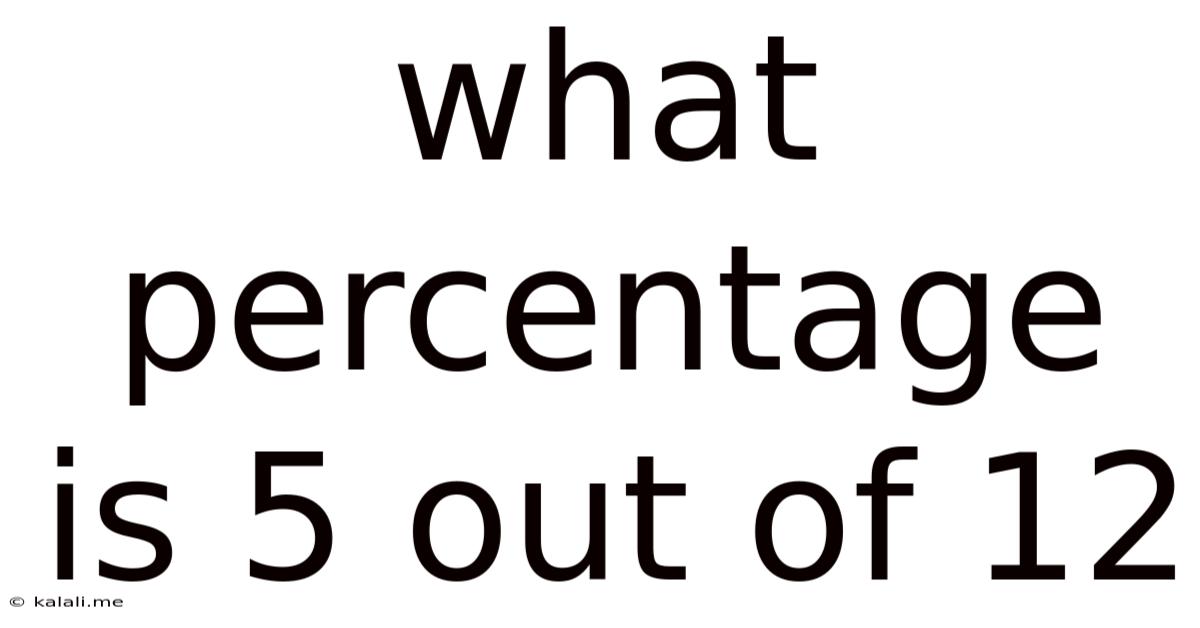
Table of Contents
What Percentage is 5 out of 12? A Comprehensive Guide to Percentage Calculations
Knowing how to calculate percentages is a fundamental skill with applications spanning various aspects of life, from everyday budgeting and shopping to more complex scenarios in finance and statistics. This article delves into the question: "What percentage is 5 out of 12?" We'll not only provide the answer but also explore the underlying concepts, different calculation methods, and real-world applications to solidify your understanding of percentage calculations. This guide will equip you with the knowledge to tackle similar percentage problems confidently.
Meta Description: Learn how to calculate percentages easily! This comprehensive guide explains how to determine what percentage 5 out of 12 represents, covering various methods and real-world applications of percentage calculations.
Understanding Percentages
A percentage is a fraction or ratio expressed as a number out of 100. It represents a portion of a whole. The symbol "%" is used to denote percentage. For instance, 50% means 50 out of 100, or one-half. Understanding percentages is crucial for interpreting data, comparing values, and understanding proportions. Many everyday situations involve percentages, such as sales discounts, interest rates, tax calculations, and more.
Calculating "What Percentage is 5 out of 12?"
There are several ways to calculate what percentage 5 represents out of 12. Let's explore the most common methods:
Method 1: Using the Fraction Method
This is the most straightforward approach. We can express "5 out of 12" as a fraction: 5/12. To convert this fraction to a percentage, we need to express it as a fraction with a denominator of 100.
-
Step 1: Set up the equation: 5/12 = x/100 (where 'x' represents the percentage we're looking for).
-
Step 2: Cross-multiply: 12x = 500
-
Step 3: Solve for 'x': x = 500/12
-
Step 4: Calculate: x ≈ 41.67
Therefore, 5 out of 12 is approximately 41.67%.
Method 2: Using Decimal Conversion
This method involves converting the fraction to a decimal and then multiplying by 100.
-
Step 1: Convert the fraction 5/12 to a decimal by dividing 5 by 12: 5 ÷ 12 ≈ 0.4167
-
Step 2: Multiply the decimal by 100 to express it as a percentage: 0.4167 x 100 = 41.67%
This method yields the same result: 41.67%.
Method 3: Using a Calculator
Most calculators have a percentage function. Simply divide 5 by 12 and then multiply by 100. The calculator will directly provide the percentage. This is the quickest method, especially for more complex calculations.
Rounding and Precision
In the examples above, we rounded the result to two decimal places (41.67%). The level of precision required depends on the context. For informal calculations, rounding to the nearest whole number (42%) might suffice. However, for financial calculations or scientific applications, higher precision is generally necessary.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is essential in numerous real-world situations:
-
Sales and Discounts: Calculating discounts on sale items, determining the final price after a percentage discount. For example, a 20% discount on a $100 item means a $20 reduction, resulting in a final price of $80.
-
Taxes: Calculating sales tax, income tax, or value-added tax (VAT) on purchases or income. If the sales tax is 8%, you'd pay an additional 8% of the item's price.
-
Interest Rates: Calculating simple or compound interest on loans or investments. Understanding interest rates helps in comparing financial products and making informed decisions.
-
Financial Analysis: Analyzing financial statements, calculating profit margins, return on investment (ROI), and other key financial metrics. Percentages provide a standardized way to compare financial performance over time or across different companies.
-
Statistics and Data Analysis: Representing data proportions, calculating percentages in surveys, polls, and other statistical analyses. Percentages make it easy to understand and interpret data trends.
-
Grading and Assessment: Calculating grades based on scores, determining percentages of correct answers on tests or quizzes. Percentage scores are a common method for assessing performance.
-
Proportions and Ratios: Solving problems involving proportions and ratios. Many real-world situations can be expressed as ratios, and converting these ratios to percentages makes them easier to understand and compare.
More Complex Percentage Problems
While the "5 out of 12" problem is relatively simple, the same principles apply to more complex scenarios. For example, consider calculating the percentage increase or decrease between two values:
- Percentage Increase: [(New Value - Old Value) / Old Value] x 100
- Percentage Decrease: [(Old Value - New Value) / Old Value] x 100
Understanding these formulas allows you to calculate percentage changes in various contexts, such as population growth, price fluctuations, or changes in sales figures.
Tips for Mastering Percentage Calculations
-
Practice Regularly: The best way to improve your percentage calculation skills is through regular practice. Work through various problems of increasing difficulty.
-
Use Different Methods: Experiment with different calculation methods to find the approach that works best for you. Some people prefer the fraction method, while others find the decimal method more intuitive.
-
Check Your Answers: Always double-check your answers to ensure accuracy. Use a calculator to verify your calculations, especially for complex problems.
-
Understand the Context: Pay attention to the context of the problem to determine the appropriate level of precision and rounding.
Conclusion
Calculating percentages is a valuable skill with wide-ranging applications. This article has comprehensively addressed the question, "What percentage is 5 out of 12?", providing multiple calculation methods and highlighting the importance of percentages in various real-world contexts. By mastering percentage calculations, you'll enhance your ability to analyze data, make informed decisions, and solve problems across many different fields. Remember to practice regularly and choose the method that best suits your understanding and the complexity of the problem at hand. With consistent practice, you will become proficient in this fundamental mathematical skill.
Latest Posts
Latest Posts
-
What Percent Is 3 Out Of 15
Apr 19, 2025
-
Cuantas Pulgadas Hay En 6 Pies
Apr 19, 2025
-
How Many Inches Is 153 Cm
Apr 19, 2025
-
What Is 50 Grams In Oz
Apr 19, 2025
-
Convert 10 Fluid Ounces Into Cups
Apr 19, 2025
Related Post
Thank you for visiting our website which covers about What Percentage Is 5 Out Of 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.