What Is 4 Percent Of 40
Kalali
Apr 24, 2025 · 5 min read
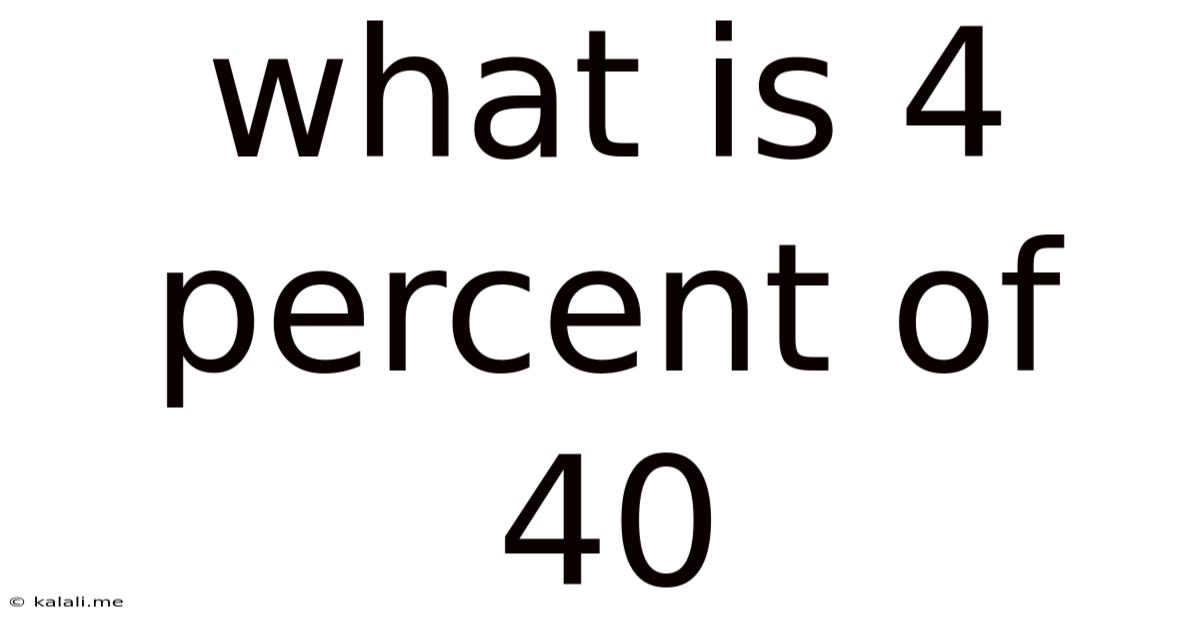
Table of Contents
What is 4 Percent of 40? A Deep Dive into Percentage Calculations and Their Real-World Applications
What is 4 percent of 40? The answer, simply put, is 1.6. But this seemingly straightforward calculation opens the door to a much broader understanding of percentages, their practical applications, and how to confidently tackle similar problems. This article will not only provide the answer but delve into the methods behind the calculation, explore various approaches to solving percentage problems, and highlight the importance of understanding percentages in numerous real-world scenarios. We will also touch upon more advanced percentage calculations and related mathematical concepts.
Understanding Percentages: A Foundation for Calculation
A percentage is a way of expressing a number as a fraction of 100. The symbol used to represent percentage is "%". Essentially, a percentage shows the proportion of a whole. For instance, 50% represents 50 out of 100, which is equivalent to 1/2 or 0.5. Understanding this fundamental concept is crucial for tackling percentage calculations accurately.
Method 1: The Basic Formula
The most common method for calculating a percentage of a number involves using a simple formula:
(Percentage/100) * Number = Result
In our case, we want to find 4% of 40. Plugging the values into the formula, we get:
(4/100) * 40 = 1.6
Therefore, 4 percent of 40 is 1.6.
Method 2: Converting Percentage to Decimal
Another effective method involves converting the percentage to its decimal equivalent before performing the calculation. To convert a percentage to a decimal, simply divide the percentage by 100. In our example:
4% / 100 = 0.04
Now, multiply the decimal equivalent by the number:
0.04 * 40 = 1.6
This method simplifies the calculation and can be particularly useful when dealing with more complex percentage problems.
Method 3: Using Proportions
The concept of proportions can also be used to solve percentage problems. We can set up a proportion to find the unknown value:
x / 40 = 4 / 100
Cross-multiplying gives:
100x = 160
Solving for x:
x = 160 / 100 = 1.6
This method is particularly helpful when visualizing the relationship between the percentage and the whole number.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is vital in a multitude of real-world situations. Here are a few examples:
-
Financial Calculations: Percentages are extensively used in finance. Calculating interest rates on loans, savings accounts, and investments all rely heavily on percentage calculations. Understanding discounts, sales tax, and profit margins also requires proficiency in percentage calculations. For example, calculating a 15% discount on a $100 item, determining the final price after adding 6% sales tax, or figuring out the profit margin on a product sold at a certain price, all involve percentage calculations.
-
Data Analysis and Statistics: Percentages are essential tools in data analysis and statistics. Expressing data as percentages allows for easier comparison and interpretation. For example, analyzing survey results, understanding market share, or interpreting economic indicators often involves representing data as percentages. This helps draw meaningful conclusions and facilitate informed decision-making.
-
Science and Engineering: In science and engineering, percentages are used to represent concentrations, efficiencies, and error margins. For instance, determining the concentration of a solution, calculating the efficiency of a machine, or expressing the margin of error in an experiment often requires percentage calculations.
-
Everyday Life: Percentages are encountered in our daily lives in various contexts. Understanding sales discounts, calculating tips, determining nutritional values on food labels, or comprehending statistics related to weather, sports, or demographics all require a working knowledge of percentages.
More Advanced Percentage Calculations
While finding 4% of 40 is relatively straightforward, more complex percentage problems might require multiple steps or a deeper understanding of mathematical concepts. For instance:
-
Finding the Percentage Increase or Decrease: This involves calculating the percentage change between two numbers. The formula is:
((New Value - Old Value) / Old Value) * 100. This is useful when comparing sales figures over time, tracking population growth, or analyzing any change in a quantifiable value. -
Calculating Percentage Points: Percentage points represent the absolute difference between two percentages, not the relative difference. For example, an increase from 20% to 25% is a 5 percentage point increase, but a 25% increase relative to the original 20%. This distinction is crucial in many financial and statistical contexts.
-
Compound Interest: Compound interest involves earning interest on both the principal amount and accumulated interest. Calculating compound interest requires understanding exponential growth and repeated percentage calculations. Understanding compound interest is fundamental for long-term financial planning.
-
Percentage Markup and Markdown: These are common terms in business. Markup refers to the percentage added to the cost price to determine the selling price, while markdown represents the percentage reduction in the selling price. These calculations are crucial for businesses to set profitable prices.
Mastering Percentage Calculations: Tips and Tricks
-
Practice Regularly: Consistent practice is key to mastering percentage calculations. Solve a variety of problems to build your confidence and speed.
-
Understand the Concepts: Don't just memorize formulas; understand the underlying principles of percentages.
-
Use Different Methods: Explore various approaches to solving percentage problems, choosing the method that works best for you in each scenario.
-
Utilize Online Resources: Many online resources offer practice problems, tutorials, and calculators to help you improve your skills.
-
Break Down Complex Problems: If faced with a complex problem, break it down into smaller, more manageable steps.
In conclusion, while the answer to "What is 4 percent of 40?" is simply 1.6, the journey to finding that answer reveals a wealth of knowledge about percentages, their various applications, and their significance in diverse fields. By understanding the different methods of calculation and their practical implications, one can confidently tackle percentage problems and apply this fundamental skill in various aspects of life, from personal finance to professional endeavors. The seemingly simple calculation serves as a gateway to a much broader and essential understanding of mathematical concepts used daily.
Latest Posts
Latest Posts
-
167 Cm In Feet And Inches
Apr 24, 2025
-
How Many Valence Electrons Do The Noble Gases Have
Apr 24, 2025
-
The Final Electron Acceptor In Aerobic Respiration Is
Apr 24, 2025
-
Which Is An Interconnection Of Food Chains In An Ecosystem
Apr 24, 2025
-
5 Is What Percent Of 9
Apr 24, 2025
Related Post
Thank you for visiting our website which covers about What Is 4 Percent Of 40 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.