What Is 5 Percent Of 50
Kalali
Apr 17, 2025 · 5 min read
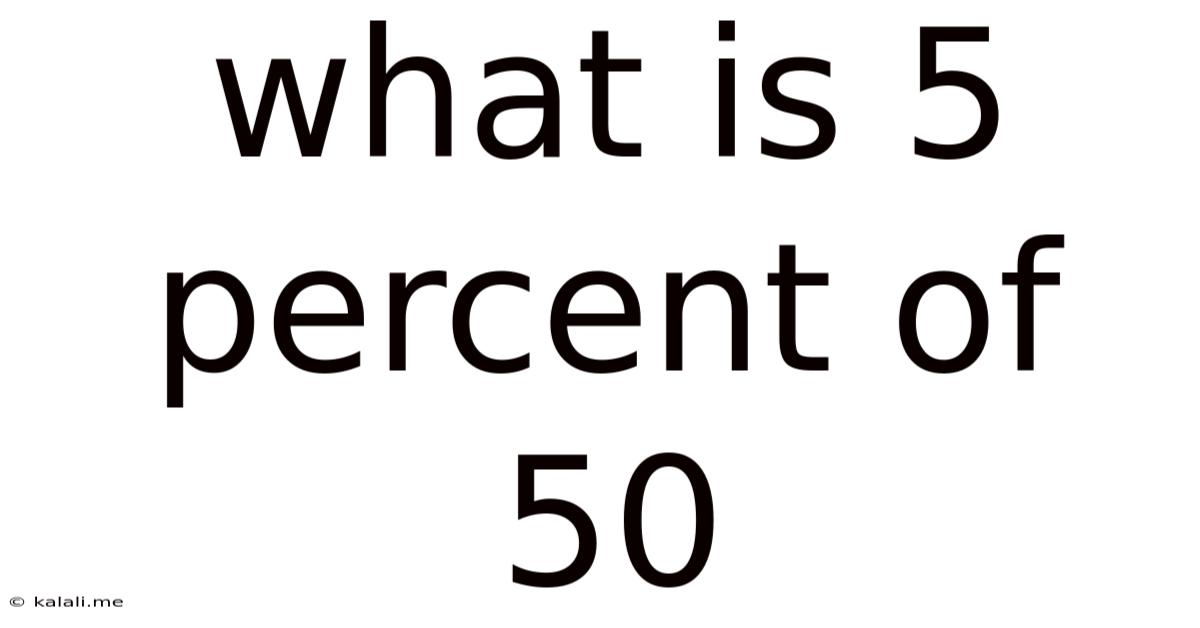
Table of Contents
What is 5 Percent of 50? A Deep Dive into Percentages and Their Applications
Finding 5 percent of 50 might seem like a simple calculation, but understanding the underlying principles of percentages opens doors to a wide range of applications in everyday life, from calculating discounts and sales tax to understanding financial reports and analyzing statistical data. This article will not only answer the question – what is 5 percent of 50? – but also explore the broader context of percentages, providing you with a comprehensive understanding of this fundamental mathematical concept.
Meta Description: Learn how to calculate 5% of 50 and delve into the world of percentages. This comprehensive guide explores various methods, real-world applications, and the importance of percentage calculations in everyday life and various professions.
Understanding Percentages: The Basics
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" literally means "out of one hundred." It's a way to express a proportion or a part of a whole. The symbol "%" represents "percent." For instance, 50% means 50 out of 100, which can be simplified to 1/2 or 0.5.
Understanding this fundamental definition is crucial for solving percentage problems. Every percentage calculation involves three key components:
- The Percentage: This is the rate or proportion being considered (e.g., 5%).
- The Whole (or Base): This is the total amount from which the percentage is calculated (e.g., 50).
- The Part: This is the result of the percentage calculation (e.g., 5% of 50).
Calculating 5 Percent of 50: Three Methods
There are several ways to calculate 5% of 50. Let's explore three common methods:
Method 1: Converting to a Decimal
This is perhaps the most straightforward method. To convert a percentage to a decimal, simply divide the percentage by 100. In this case:
5% / 100 = 0.05
Then, multiply the decimal by the whole number:
0.05 * 50 = 2.5
Therefore, 5 percent of 50 is $\boxed{2.5}$
Method 2: Using Fractions
Percentages can also be expressed as fractions. 5% can be written as 5/100, which simplifies to 1/20. To find 5% of 50, we multiply the fraction by the whole number:
(1/20) * 50 = 50/20 = 2.5
Again, we arrive at the answer: $\boxed{2.5}$
Method 3: Proportion Method
This method utilizes the concept of ratios and proportions. We set up a proportion:
5/100 = x/50
Cross-multiplying, we get:
100x = 5 * 50
100x = 250
x = 250/100 = 2.5
The result is, once more, $\boxed{2.5}$
Real-World Applications of Percentage Calculations
Understanding percentage calculations is essential in numerous real-world scenarios. Here are a few examples:
- Sales and Discounts: Stores often advertise discounts as percentages (e.g., "20% off"). Calculating the discount amount requires finding the percentage of the original price.
- Taxes: Sales tax, income tax, and other taxes are often expressed as percentages. Calculating the tax amount requires finding the percentage of the taxable amount.
- Tips and Gratuities: When dining out, it's customary to leave a tip, often expressed as a percentage of the bill.
- Financial Analysis: Investors use percentages to analyze financial statements, calculate returns on investment, and assess risk.
- Statistics: Percentages are used extensively in statistics to represent proportions and probabilities. For example, expressing the percentage of people who prefer a particular product.
- Science and Engineering: Percentage calculations are utilized in various scientific fields, such as determining the concentration of solutions or expressing the efficiency of a machine.
Beyond the Basics: More Complex Percentage Problems
While calculating 5% of 50 is relatively simple, percentage problems can become more complex. Here are a few examples:
- Finding the Percentage: Instead of finding a percentage of a number, you might need to find what percentage one number is of another. For example, "What percentage of 80 is 20?" This requires setting up a proportion or dividing the part by the whole and multiplying by 100.
- Finding the Whole: You might know the percentage and the part, but need to find the whole. For example, "If 15 is 25% of a number, what is the number?" This involves setting up an equation and solving for the unknown.
- Percentage Increase and Decrease: These calculations involve determining the percentage change between two values. The formula for percentage increase is: [(New Value - Old Value) / Old Value] * 100. The formula for percentage decrease is similar but subtracts the new value from the old value.
- Compound Interest: This involves calculating interest on both the principal amount and accumulated interest. It's a more advanced percentage calculation frequently used in finance.
Mastering Percentages: Tips and Practice
To master percentage calculations, regular practice is key. Start with simple problems like the one we've discussed – finding 5% of 50 – and gradually work your way up to more complex problems. Here are some tips:
- Understand the Fundamentals: Ensure you have a solid grasp of the basic concepts of percentages, fractions, and decimals.
- Practice Regularly: Solve various percentage problems to build your skills and confidence.
- Use Different Methods: Try different calculation methods to find the approach that works best for you.
- Check Your Work: Always double-check your answers to ensure accuracy.
- Utilize Online Resources: Many online resources, including calculators and tutorials, can help you learn and practice percentage calculations.
Conclusion: The Significance of Percentage Understanding
The seemingly simple calculation of 5% of 50 serves as a gateway to understanding the broader world of percentages. From everyday transactions to complex financial analyses, the ability to work with percentages is a valuable skill applicable across numerous fields. By mastering these concepts, you enhance your analytical abilities and improve your capacity to navigate the quantitative aspects of modern life. So, next time you encounter a percentage problem, remember the fundamentals, practice different methods, and you'll find yourself confidently calculating percentages in any situation. The answer to "What is 5 percent of 50?" – 2.5 – is just the beginning of your journey into the world of percentage mastery.
Latest Posts
Latest Posts
-
What Are The Agents Of Erosion
Apr 19, 2025
-
How Many Cups Is 16 9 Oz Of Water
Apr 19, 2025
-
What Percentage Is 18 Of 24
Apr 19, 2025
-
How Hot Is 90 Degrees Celsius
Apr 19, 2025
-
Cuanto Es 18 Libras En Kilos
Apr 19, 2025
Related Post
Thank you for visiting our website which covers about What Is 5 Percent Of 50 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.